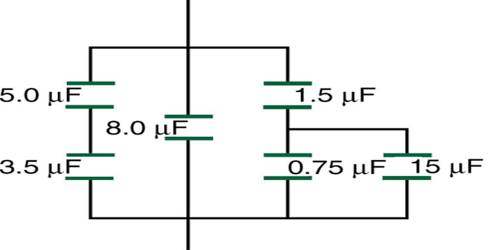
Series combination of Equivalent capacitance
Series combination: When some capacitors are connected in such a way that the second plate of the first capacitor is connected to the first plate of the second capacitor and the second plate of the second capacitor is connected to the first plate of the third capacitor and so on and the end plate of the last capacitor is connected to the ground, then the combination or grouping is called series combination.
All the plates in series combination except the last plate of the last capacitor remain insulated from the ground. In fig, C1, C2, and C3 are capacitances of three capacitors AB, CD, and EF. These capacitors are connected in series.
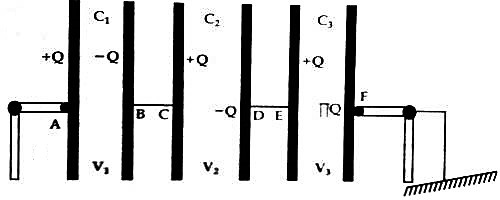
If Q amount of positive charge is given to the first plate A of the first capacitor AB, then the same amount of negative charge will be induced in the second plate B and the same amount of positive charge will be induced in the plate C of the capacitor CD. Negative charge Q of the same amount will be induced in the second plate D of the second capacitor CD. This process of induction will continue and the end plate of the last capacitor will be negative. Now the second plate of the first capacitor is connected to the first plate of the second capacitor: so their potentials will be same. Similarly, the potential of the second plate of the second capacitor and the first plate of the third capacitor will be same. Let the potential difference between the plates of the first, second and third capacitors be respectively V1, V2, and V3 and let the potential difference between the first plate A and the last plate F of the combination be V.
Then V = V1 + V2 + V3.
Again, V1 = Q/C1; V2 = Q/C2; and V3 = Q/C3
So, V = Q/C1 + Q/C2 + Q/C3 = Q (1/C1 + 1/C2 + 1/C3) … … … … (1)
But instead of the series combination a capacitor of capacitance CS is used and Q amount of charge is given to the first plate of this capacitor, then the potential difference between this plate and the grounded plate is,
V = Q/CS … … … (2)
From equations (1) and (2) we get,
Q/CS = Q (1/C1 + 1/C2 + 1/C3)
So, 1/CS = (1/C1 + 1/C2 + 1/C3)
CS is the equivalent capacitance.
Similarly, it can be shown that if n number of capacitors of capacitances C1, C2, C3, … … Cn, are connected in series, then the equivalent capacitance will be,
1/CS = 1/C1 + 1/C2 + 1/C3 + … … + Cn = Σ 1/C
So, in series combination, the summation of the reciprocal of individual capacitance of the capacitors is equal to the reciprocal of the equivalent capacitance.