Rules of Geometrical Addition of Vectors
Geometrical Method: Two similar vectors can be added or subtracted. For example, displacement can be added only with displacement. Question does not arise to add or subtract displacement with velocity.
A vector quantity has both magnitude and direction. So, addition or subtraction of vector quantities is not done by usual algebraic rule. Directions of vectors create problem in this case.
For example let the velocity of the wheel of a boat be 8 km/hr. and the velocity of water-current is 6 km/hr. If the boat is allowed to move directly from one bank of the river to the opposite bank, the velocity that will act on the boat will not be equal to the algebraic addition of (8+6) = 14 km/hr. This will not give actual velocity-actual velocity will be totally different. Besides, the direction of the boat will be between the directions of the two velocities. For this reason, addition and subtraction of vector quantities are done following geometrical method.
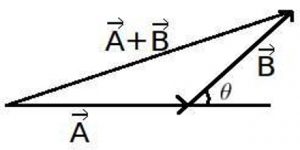
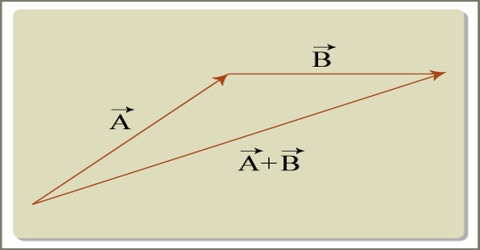
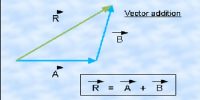
There are many ways of combining vectors or adding and subtracting vectors. The simplest and most straight forward method of combining vectors is by graphical method or geometrical method. In order to add two like vector quantities, the quantities are to be directed along the same direction, on the other hand for subtraction the quantities are to be directed opposite to each other. But if two or more vectors act at the same point, their addition will be a new vector. This new vector formed due to addition of two or more sectors is called the resultant of these vectors.
Geometrical Addition of Vector Quantities
Addition of vectors can be done by the following five laws:
(i.) General law
(ii) Law of triangle
(iii) Law of polygon
(iv) Law of parallelogram and
(v) Law of components.