Relation between Stress–Strain
The magnitude of the action or reaction per unit area of the object is called stress. That means, stress is measured by the force per unit area of a body. On the other hand, strain may be measured by the change produced in unit dimension of a body. This strain may be change in length, size, area or volume. Relation between stress and strain may be expressed by graph and mathematical method.
Graphical Representation for Stress-Strain Relationship
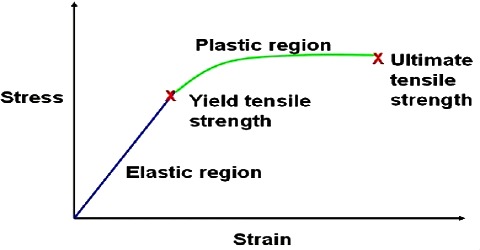
The relationship between stress and strain may best be studied by plotting a graph between the two for various values of stem and the accompanying strain. Let a wire of a solid material is taken and increasing loads are gradually placed on one end of the wire. The other end of the wire remains rigidly fixed to a support. As the load increases the elongation of the wire also increases. Now stress and strain are calculated for different values of loads and elongations and a graph of stress and strain is drown. In this graph strain is plotted along X-axis and stress along Y-axis [Figure].
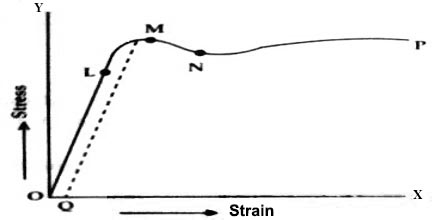
In fig, O is the origin where stress is zero, so strain is also zero. From O to point L, the graph is a straight line. Here stress and strain are proportional to each other i.e., as the stress increases, strain also increases proportionately. Upto OL the wire will be fully elastic i.e., if stress is withdrawn strain decreases to zero. So the force associated with this stress is the elastic limit. Beyond OL the wire will not remain perfectly elastic.
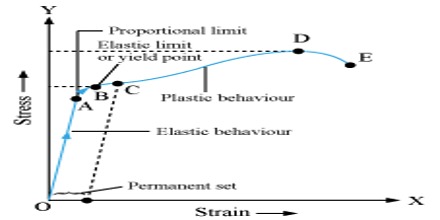
Now, if stress is increased further the strain will increase more rapidly. In this situation, rate of increase of stress will be more than that of strain i.e., if stress is withdrawn the wane wall not return to its original condition. There will be permanent strain in the wire. In figure OQ represents permanent deformation. This state will continue upto point M. The poind is called yield point. Afterward, strain continues to increase upto N even though stress is not increased. If the stress is increased further, the wire will be thinner in many places and finally the wire will snap. The point at which snap occurs is called its breaking point. In the graph, P is the breaking point. The stress at point P is called breaking stress.
Definition of breaking stress can be written as, “The minimum force per unit area of a body for which the body breaks or snaps is called breaking stress.”
By multiplying breaking stress with area of cross-section of the wire breaking weight or breaking force at obtained. It is to be mentioned that it the stress is applied for a long time on an object; it may develop permanent strain even though the stress is below the elastic limit.