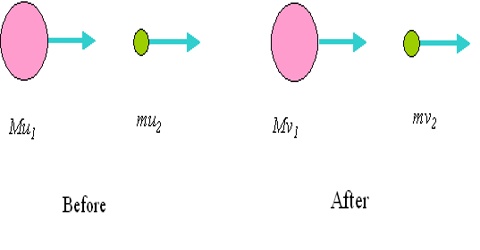
Principle of conservation of momentum
From Newton’s third law of motion we can know about the conservation principle of momentum. Principle of conservation of momentum is equally applicable for all bodies— small or large, earthly or terrestrial. From Newton’s first law of motion we know that if net applied force on a body is zero, then a moving body will continue its motion with uniform speed along a straight line i.e., its speed remains constant. If velocity v is constant with respect to time then momentum p = m v and remains constant with respect to time. In other words it can be said that if no external force is active on a body or net force is zero, then total momentum remains constant. If objects collide, the total momentum before the collision is the same as the total momentum after the collision (provided that no external forces – for example, friction – act on the system). This is the principle of conservation of momentum.
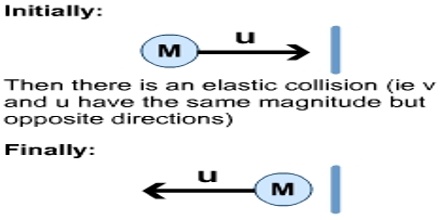
In physics, the principle of conservation of momentum states that when you have an isolated system with no external forces, the initial total momentum of objects before a collision equals the final total momentum of the objects after the collision. The term conservation refers to something which doesn’t change. This means that the variable in an equation which represents a conserved quantity is constant over time. It has the same value both before and after an event.
For example, a coin sliding on a table experiences a friction force. If you give it some speed and let it go it spontaneously stops. In the theory that takes only the coin into account, the momentum is not conserved. Of course the momentum hasn’t disappeared. It went in imperceptible movement of the table, the ground, etc which were neglected.