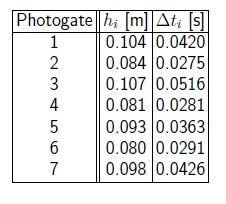
Example: A steelball with mass in = 0.44 kg and radius r = 1.0 cm moves along a rollercoaster. Seven photogates are placed along the track at different heights hi from the base of the track; we measure the time intervals Δti for the steel ball to pass through each photogate,
 Calculate the gravitational potential energy, kinetic energy, and total mechanical energy.
Calculate the gravitational potential energy, kinetic energy, and total mechanical energy.
Solution: We have the gravitational potential energy PEi = mghi. The (average) speed of the ball is vi = 2r/Δti, as it passes through each photogate. The kinetic energy then follows KE = mvi2/2. Note that the steel ball moves along the track (translational motion), but also rotates [rotational motion]. As a result, the kinetic energy of the ball has a contribution from rotation. In this situation, the contribution of rotational kinetic energy can be described by an “effective” mass m*, greater than the mass in. If the track has a width w = 0.95 cm, we find,
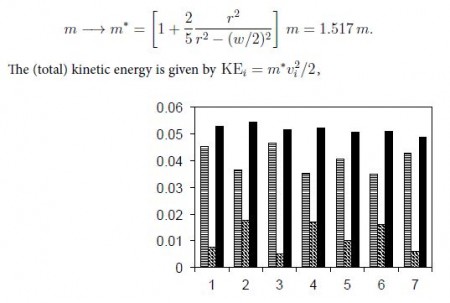
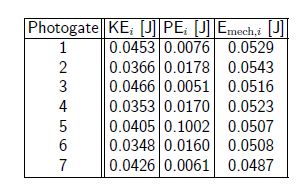
Discussion: The mechanical energy of the system (slightly) decreases due to friction.












