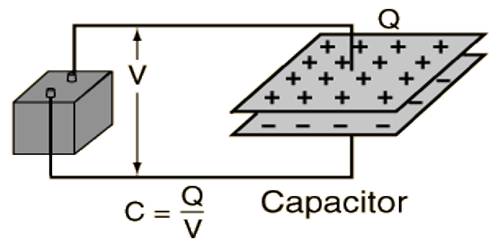
Potential energy of a capacitor
Suppose a piece of brick is kept above the roof, or water is pumped in a tank placed on the roof. In both the cases, the brick and water have acquired some energy. This type of energy is called potential energy. The mechanical process of storing charges in a conductor is called capacitor or, the mechanical process by which electricity is stored is called capacitor. A capacitor is formed by two conductors separated by a small distance.
Let one plate of a capacitor be earthed and the other plate is charged with a potential V. The work done in charging the capacitor is stored as potential energy in the capacitor. In this case, the work done in charging the plate to the potential V is the necessary work to charge the capacitor and it is the potential energy of the capacitor.
While charging the plate, let V be the potential at any instant, work done to add ‘dq’ amount of charge to the plate at that time is,
dW = Vdq = q/C dq
The total work done in charging the plate from 0 to Q is,
W = ∫dW = Q∫0 q/C dq, here, C is the capacitance of the capacitor.
or, W = 1/C [q2/2]Q0 = 1/C [Q2/C] = ½ Q2/C
Potential energy, P.E. = W = Q2/2C …. …. ….. (1)
= ½ QV … … … (2) (as we know, V = Q/C)
= ½ CV2 … … … (3)
If Q is expressed in coulomb, V in volt and C in farad, then potential energy will be in Joule (J). Each of the equations, (1), (2) and (3) represents the potential energy of a capacitor.
Potential energy per unit volume of a capacitor in an electric field
It may be considered that the energy of the capacitor remains stored in the electric field between the plates at the capacitor. Now, we will determine the energy per unit volume at any point in the electric field. Let the energy per unit volume be u,
So, u = W / volume = W/Ad
Here, A is the area of a plate and d, the distance between the plates; i.e., Ad is the volume of the space between the plates of the capacitor.
From equation (3), we get,
u = ½ CV2 / Ad = ½ C(Ed)2 /Ad [V = Ed]
Using equation [Capacitance of Parallel Plate Capacitor or condenser] we get,
u = [½ (ε0A / d) x (Ed)2] / Ad
= ½ ε0E2 … … … (1)
For any dielectric medium of dielectric constant εr between the plates of the capacitor, the potential energy per unit volume is,
u = ½ εrε0E2 = ½ εE2 … … … (2) [εrε0 = ε]
It is to be noticed that in equations (1) and (2) area and distance are not included, so those equations are valid for any geometrical shape of the capacitor.