Potential of a charged sphere
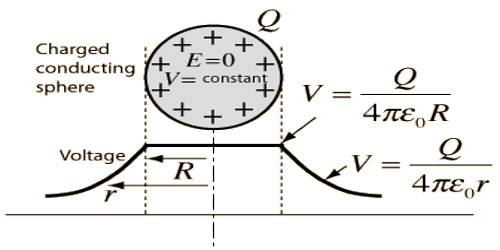
Consider a charged sphere with a symmetrical distribution of charge. Gauss’ Law tells us that the electric field outside the sphere is the same as that from a point charge. This implies that outside the sphere the potential also looks like the potential for a point charge.
Let A be a sphere of radius r (Fig. a). If +q amount or charge is given to it, the charge will spread all over the surface of the sphere. All field lines from the surface of the sphere will travel perpendicular to the surface along straight lines.
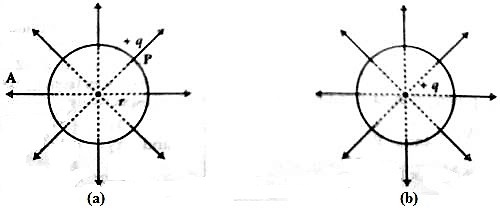
If these lines are drawn backward these will meet at the center of the sphere. Now, if we consider that charge + q is located at this centre, then similar lines of force will emerge through the surface of the sphere in all directions [Fig. (b)]. So, from any consideration the amount of charge may be considered as centered at the centre of the sphere. So the potential V at point P at the surface of the sphere in air medium is,
V = charge/distance = (1 / 4πε0) x (q/r)
and electric field intensity, E = (1 / 4πε0) x (q/r2)
But surface charge density of the sphere, σ = q/A = q / 4πr2
then, Electric field, E = (1 / 4πε0) x (q/r2) = q / ε04πr2 = q / ε0A
or, E = σ/ε0
Potential at any point inside the sphere is equal to the potential at the surface. This is because that if potential at the surface be V and potential at any point inside the sphere is V0, then V – V0 = electric field intensity x distance = 0. [as, E = 0 inside the sphere]
V = V0
Hence, the potential at the surface of the sphere or inside the sphere, V = (1 / 4πε0) x (q/r)
At any other medium having dielectric constant, εr, V = (1 / 4πε0εr) x (q/r)