When gravity is taken into account, Pascal’s law is to be modified. Consider a cylindrical liquid column of height It and density ρ in a vessel as shown in the Figure.
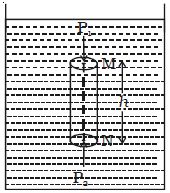
If the effect of gravity is neglected, then the pressure at M will be equal to the pressure at N. But, if force due to gravity is taken into account, then they are not equal. As the liquid column is in equilibrium, the forces acting on it are balanced. The vertical forces acting is-
(i) Force P1A acting vertically down on the top surface.
(ii) Weight mg of the liquid column acting vertically downwards.
(iii) Force P2A at the bottom surface acting vertically upwards, where P1 and P2 are the pressures at the top and bottom faces. A is the area of the cross-section of the circular face and m is the mass of the cylindrical liquid column.
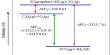
At equilibrium, P1A + mg – P2A = 0
Or, P1A + mg = P2A
So, P2 = P1 + (mg/A)
But, m = Ahρ
Then, P2 = P1 + (Ahρg/A)
Therefore, P2 = P1 + hρg
This equation proves that the pressure is the same at all points at the same depth. This results in another statement of Pascal’s law which can be stated as the change in pressure at any point in an enclosed fluid at rest is transmitted undiminished to all points in the fluid and act in all directions.