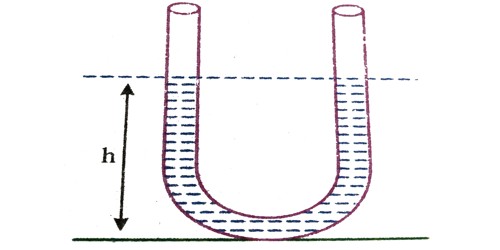
Consider a non-viscous liquid column of length/of uniform cross-sectional area A (Figure). Initially, the level of liquid in the limbs is the same. If the liquid on one side of the tube is depressed by blowing gently the levels of the liquid oscillate for a short time about their initial positions O and C, before coming to rest.
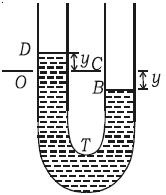
If the liquid in one of the limbs is depressed by y, there will be a difference of 2 y in the liquid levels in the two limbs. At some instant, suppose the level of the liquid on the left side of the tube is at D. at a height y above its original position O, the level B of the liquid on the other side is then at a depth y below its original position C. So the excess pressure P on the liquid due to the restoring force is: excess height x density x g
Pressure = 2 y ρ g
Force on the liquid = pressure x area of the cross-section of the tube = – 2yρg x A … … (1)
The negative sign indicates that the force towards O is opposite to the displacement measured from O at that instant.
The mass of the liquid column of length 1 is: volume x density
(i.e) m = l A ρ
F= l A ρ a … … (2)
From equations (1) and (2), l A ρ a = – 2 y A ρ g
So, a = (2g/l)y … … (3)
We know that; a = – ω2y
Here, the acceleration is proportional to the displacement, so the motion is simple harmonic and the period T is,
T = 2π/ω = 2π √(l /2g)
[The results of a combined theoretical, mathematical and experimental study of liquid oscillations in an asymmetric U-tube are presented. The configuration under research is analogous to that of the tuned liquid-column damper used to suppress oscillatory motion in large semi-supported structures.]
Key Concept:
In hydrostatics, pressure measurement with U-gauges and their relationship to density is a well-known experiment. If the liquid in U-tube is filled to a height ‘y’ and cross-section of the tube is uniform and the liquid is incompressible and non-viscous. Primarily the level of liquid in the two limbs will be at a similar height equal to ‘y’. Very little is studied or experimented with the dynamics of the movement of a liquid in a U-tube possibly due to its theoretical difficulty but, after all, it is a simple damped oscillating system.
The motion of an oscillating liquid column in a U-tube is
- periodic but not simple harmonic
- non-periodic
- simple harmonic and time period is independent of the density of the liquid
- simple harmonic and time period is directly proportional to the density of the liquid.