Newton assumed that sound waves travel through the air under isothermal conditions (i.e) temperature of the medium remains constant. According to Newton, when sound waves propagate in air, compression and rarefaction are formed.
The change in pressure and volume obeys Boyle’s law.
PV = constant [where, P = pressure; V = volume of air]
Differentiating, P.dV + V.dP = 0
dV = -V dP
So, P = -dp / (dV/V)
P = k (volume elasticity), therefore under isothermal condition, P = k
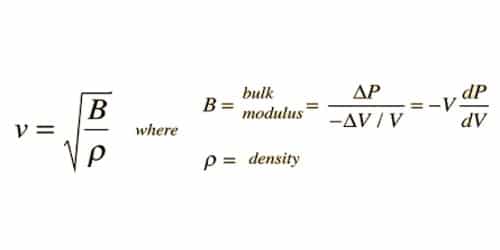
then, V = √(k/ρ) = √(P/ρ)
where P is the pressure of air and ρ is the density of air. The above equation is known as Newton’s formula for the velocity of sound waves in a gas. Relationship of velocity or air with bulk modulus and density. This is the required expression for the velocity of sound in air.
At NTP, P = 76 cm of mercury
= (0.76 x 13.6 x 108 x 9.8) N m-2
ρ = 1.293 kg m-3.
The velocity of sound in air at NTP is;
V = √[(10.76 x13.6 x108 x 9.8) / 1.293]
= 280 ms-1
The experimental value for the velocity of sound in air is 332 m s-1. But the theoretical value of 280 m s-1 is 15% less than the experimental value. This discrepancy could not be explained by Newton’s formula.
Newton assumed that the procedure is very sluggish and the heat produced during density is given to surrounding and heat loss during compression is gained from the surrounding. So the temperature remains steady and sound waves propagate through an isothermal procedure. That is, the heat produced during compression (pressure increases, volume decreases), and heat lost during rarefaction (pressure decreases, volume increases) occur over a period of time such that the temperature of the medium remains constant.
Calculation of Velocity of air –
Now, the velocity of sound in air using Newton’s formula at NTP (Normal Temperature and Pressure) is given by:
Pressure (P)= 1.1013 * 105 N/m2
Density of air (ρ) = 1.293 kg/m3
Calculation of velocity of sound in air with Newton’s formula.