Motion in Opposite Direction

Motion in Opposite Direction

If two bodies start moving opposite to each other and if the velocity v_A of the body ‘A’ is considered positive, then velocity v_B of the body ‘B’ is to be taken as negative.

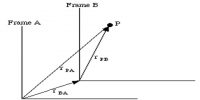
Example (A): Look at the two figures below. In the first figure two cars are moving in the same direction [Fig (a)] and in the second figure, they are moving opposite to each other. How will you determine the relative velocity between them? Here, in case of two parallel linear motion, the following two motions are to be considered for determining relative velocity.

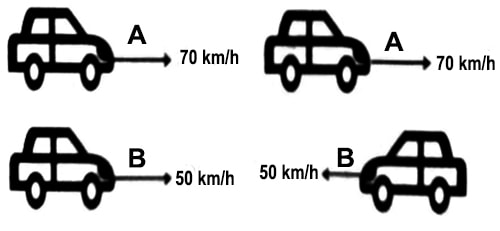
Here the relative velocity of ‘A’ with respect to ‘B’ will be,

v_AB = v_A – (- v_B) = v_A + v_B; if v_A ≥ v_B.

So, looking from the body ‘B’ it will appear that the both ‘A’ is approaching towards or moving away from B with velocity v_AB. Since v_BA = – v_B – v_A = – (v_B + v_A), so looking from the body ‘A’ the body ‘B’ will appear that the body B is approaching towards ‘A’ or moving away from it.

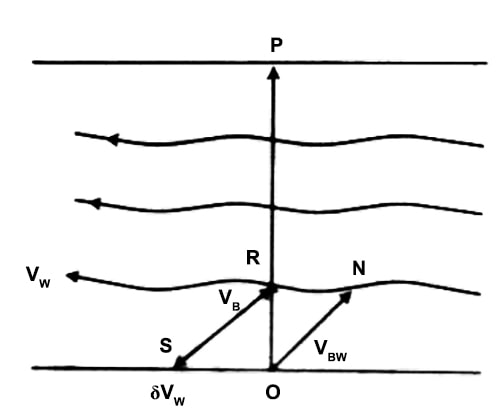
Example (b): Suppose a person from one side of a river at point O wants to go by boat exactly to the opposite side of the river at point P, then the person is to row the boat in the direction ON (Fig).

If the relative velocity of the boat with respect to current is v_BW and the velocity of the current is v_w, then their vector summation will give a velocity of the boat, i.e., v_B^→ =v_W^→ + v_BW^→.

Conclusions: Following conclusions may be drawn from the above example:

(1) If two bodies move in the same direction, then by subtracting their velocities relative velocity can be obtained.

(2) If two bodies move in the opposite direction, then the relative velocity is obtained by addition of the velocities.