Example 1: A block with mass M = 5.1 kg sits on a massless plank of length L = 2.3 m. The plank is supported on its left and right ends by cones. The block sits 1.9-m away from the left cone.
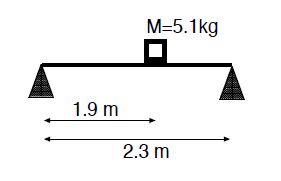 a) Draw the appropriate free-body diagram for the problem in terms of mechanical equilibrium.
a) Draw the appropriate free-body diagram for the problem in terms of mechanical equilibrium.
b) (i) Write down Newton’s second law for the plank; and (ii) choose an axis of rotation and write down the torque about that axis.
c) Find the forces that the cones exert on the plank.
d) If the support forces by the left and right cones are in a ratio of two-to-one, i.e., FL/FR = 2, where is the block placed?
Solution: Note W = Mg = 5.1 kg . 9.8 m/s2 = 50.0 N, we have
a) We have Newton’s second law:
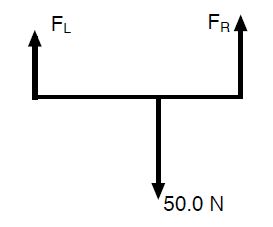
∑ F = FL + FR – 50.0 N = 0
(ii) we choose the left end of the plank as the axis of rotation, so that
∑ τ = – 50.0 N * 1.9 M + FR * 2.3 M = 0
We have
FR = (50.0 N • 1.9 m) / 2.3 m = 41.3 N
So that,
FL = 50.0 N — 41.3 N = 8.7 N.
In the case FL = 2FR so that
FL + FR = 3FR = 50.0 N → FR = 50.0 N / 3 = 16.7 N.
We use x for the distance of the block from the left side of the plank. Then,
τ = 50.0 N * x + 16.7 N • 2.3 N = 0 → x = (16.7 N * 2.3N) / 50.0N = 0.77 m.
Example 2: A wooden board with length L = 1.20 m and mass M = 3.4 kg is supported by one leg at the distance d = 0.85 m from the left end of the board, and a cable anchored to the floor at 1.9 m from the left end of the board. The length of the leg is 1.4 m.
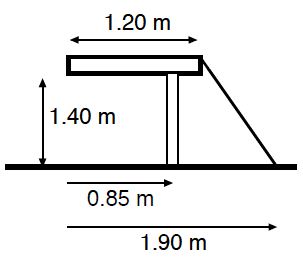
a) Draw the free-body diagram for the problem in terms of mechanical equilibrium.
b) Write down Newton’s second law for the board.
c) Choose an axis of rotation and write down the torque about that axis.
d) Find the tension in the cable.
e) What is the magnitude of the force ‘exerted by the leg on the board?
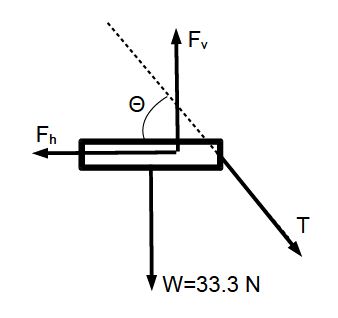
Solution: The angle of the cable with respect to the horizontal is tan θ = (1.4 m)/(0.7 = 2, so that θ = 63.4°. We have the the weight of the table W = Mg = 33.3 N; the forces from the leg Fh and Ft, and the tension on the cable T are determined by
∑ Fx = Fh – T cos 63.4° = 0,
∑ Fy = -T sin 63.4° + Fv, – 33.3 N = O.
We choose the point of contact of the leg with the board as the axis of rotation. Then,
∑ τ = 33.3N • 0.25 m — T • 0.35 m sin 63.4° = 0.
Since 0.35 m sin 63.4° = 0.31 m, we have the equation for the torque,
T = (8.3 N • m / 0.31 m) = 26.8N
We see
Fv= 33.3 N + 26.8 N • sin 63.4° = 57.3 N,
Fh = 26.8 N • cos 63.4° = 12.0 N.
We thus get for the magnitude of the force exerted by the leg,
Flog = √ (Fh2 + Fv2) = √ (12N)2 + (57.3 N)2 = 58.5 N.