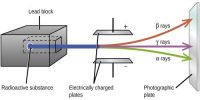
Mean Life or average life of a Radioactive Element
We know, radioactivity is a spontaneous phenomenon. It obeys the exponential law and the life of an atom can be from zero to infinity (∞). So it is possible to determine the mean life of a radioactive substance. So the life of radioactive atoms ranges from 0-infinity mean life gives the sum of the life of all the atoms to the total no. of atoms present initially.
The life which is obtained when the summation of the life of each radioactive atom divided by the initial number of atoms is called the mean or average life of that radioactive substance. This time interval may be thought of as the sum of the lifetimes of all the individual unstable nuclei in a sample, divided by the total number of unstable nuclei present.
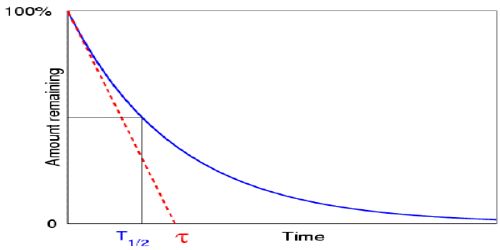
Generally, mean life or average life is designated as τ.
So, τ = (Life of 1st Atom + life of 2nd Atom + … + life of N0th atom) / N0
Mathematically, it can be shown that, τ = 1/λ = T/0.693 … … (1)
From equation (1) it is seen that average or mean life is proportional to half-life.
Mathematical Example:
The half-life of uranium is 45 x 108 years. Calculate its average life.
Here, Half-life, T = 45 x 108 yrs
Average life, t =?
We know, Average life, τ = 1/λ
Again half life, T = 0.693/λ
then, τ = 1/λ = T/0.693 = (45 x 108 / 0.693) yrs
= 64.9 x 108 yrs.