Suppose two vectors P and Q are acting simultaneously at a point making an angle α. Now according to parallelogram law the magnitude of the resultant.
R = √(P2 + Q2 + 2PQ cosα)
From the above equation it is evident that R depends on the angle between P and Q i.e., on α.
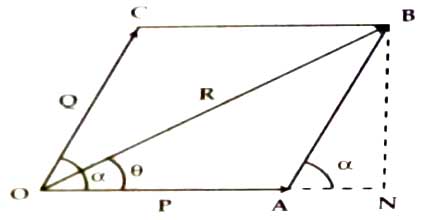
Maximum value of the resultant: R will be maximum when cos α will be maximum i.e., when cos α = l = cos 00.
or, α = 00
R(maximum) = √(P2 + Q2 + 2PQ cos00)
= √(P + Q)2
= (P + Q)
Thus, when two vectors act along the same straight line then the magnitude of the resultant will be maximum. The magnitude will be the sum of the vectors. In other words, we can say that magnitude of the resultant cannot be greater than the summation of the vectors.