Mathematical Expression for Intensity of Wave
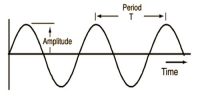
Suppose, a progressive wave is travelling along positive x-direction with constant velocity v. Due to wave motion particles of the medium will vibrate with simple harmonic motion about their equilibrium positions. If at instant t displacement of a particle is y, the equation of the motion of the particle is, y = a sin ωt, here ‘a’ is the amplitude. If frequency of the wave is n, then ω = 2πn.
Energy of a particle executing simple harmonic motion consists of two parts – one part is kinetic energy and the other part is potential energy. But at equilibrium potential energy is zero, so the total energy, in this case, is kinetic energy. Hence, if v0 is the velocity of a particle of m, then its kinetic energy is: ½ mv02. But, v0 = aω = 2πna.
So, total energy of the vibrating particle is;
½ mv02 = ½ ma2ω2 = 2π2n2a2m.
Let the particle per unit of the medium through which the wave is propagating is N. So, energy of all the particles in a unit value i.e., energy density of the wave is,
E = N (½mv02) = 2π2n2a2m N
But, mN = ρ, density of the medium.
Total energy, E = 2π2n2a2ρ
In unit time the wave travels a distance v. So, energy passing through unit area placed normal to the direction of propagation i.e., intensity of the wave, I, is equal to the energy in a cylinder, C having unit area of cross-section and length v (Figure).
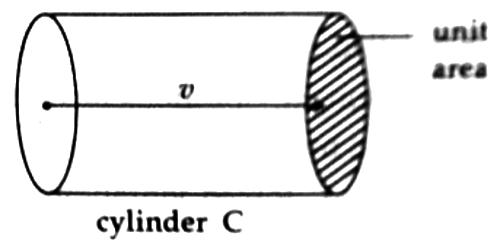
So, intensity of the wave, I = density of energy x value of the cylinder C
or, I = E x v = 2π2n2a2ρv
It is seen from this equation that intensity of wave is,
- proportional to the square of amplitude.
- proportional to the square of frequency
- proportional to the velocity and
- proportional to the density of medium.