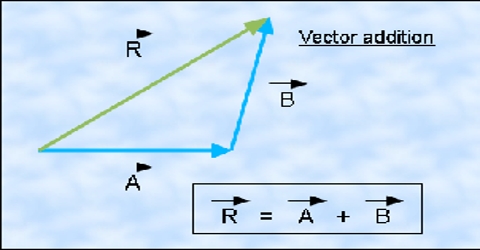
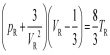Law of components of vector additions:
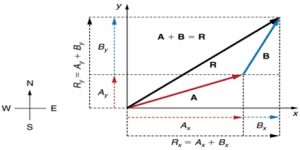
In any coordinate system a vector quantity can be resolved into components. Determine the resultant vector by resolving each vector quantity in its components and then adding by algebraic rule.
If OX, OY, OZ are three axes in three dimensional coordinate system, coordinates of the position vector R is (Ax, Ay, Az) and its components along X, Yand Z axes are Axî, Ayĵ and Azƙ; then
Ā = Axî + Ayĵ + Azƙ
Similarly, the vector B can be written along X, Y and Z axes in terms of components as,
B = Bxî + Byĵ + Bzƙ
Addition of these two vectors is: R = A + B
Modulus of the resultant: Modulus at the resultant of vector addition of Ā and B is,
|C| = | A + B | = √(Cx2 + Cy2 + Cz2)
= √[(Ax+Bx)2 + (Ay+By)2 + (Az+Bz)2]
Following the above rule subtraction of the two vectors can be determined.