Kepler’s Law about Motion of the Planets
From ancient time scientists had the keen interest in the motion of planets. In sixteenth-century Tycho-Brahe, a Danish astronomer observed the motion/movement of Mars carefully and collected some information. Based on his research-oriented data and other observations in 1618 another astronomer of Denmark Johann Kepler came to the conclusion that by the influence of some force planets are continuously rotating keeping the sun at the centre. In 1619 he had formulated three laws about the planetary motion. These three laws are named after him as the Kepler’s laws of planetary motion. These laws are stated below:
- Law of the ellipse: The orbit of each planet is an ellipse which has the sun at one of its foci.
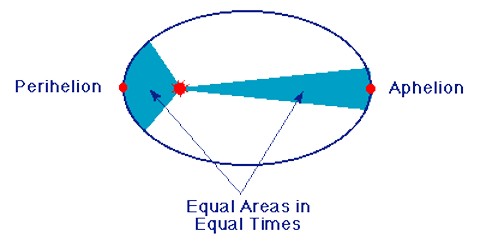
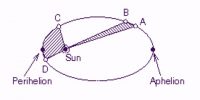
- Law of the area: Each planet moves in such a way that the imaginary line joining it to the sun sweeps out equal areas in equal times.
- Law of time: The square of the period of revolution of any planet around the sun is proportional to the cube of its mean distance from the sun.
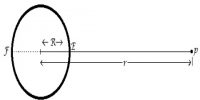
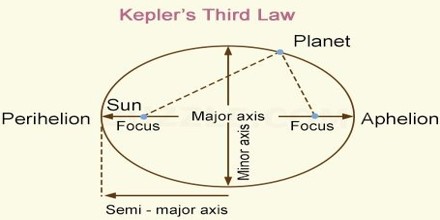
Explanation of the first law: The law gives the idea regarding the nature of the orbit of planets around the sun. Let S and S’ due two foci of an ellipse. Let the sun is at the focus S [Figure]. Now according to the first law of Kepler, each planet rotates around the ellipse keeping the sun at S.

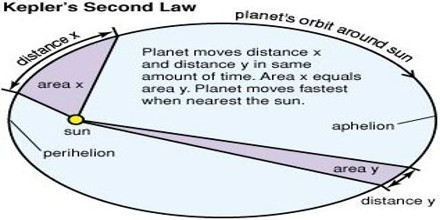
Explanation of the second law: This law establishes the relation between orbital velocity and the distance between the sun and the planet. Let the planet at time t travel from position P to Q. If that planet travels in the same time from position M to R, then according to Kepler’s second law, the area of PQS must be equal to the area of MSR.
Explanation of the third law: This law establishes the relation between planet’s orbital configuration and time of the revolution. Let The the time period of the planet i.e., time to revolve around the sun once and if 2a is the length of the major axis then according to this law,
We get,
T2 ∞ (2a)3 ∞ 8a3
Since 8 is consist, so T2 ∞ a3
From the above equation thud law of Kepler can be written with some modification as –
The time period of each planet is proportional to the half of the cube of the major axis of the orbit.
From the above law, it is seen that if the time period of rotation of a planet and the average distance are known, then by observing the time period of rotation of another planet the average distance between the sun and that planet can be determined.
Following matters are observed on the analysis of Kepler’s laws:
(1) The time period of a planet does not depend on its mass.
(2) Smaller the avenge distance between the sun and the planet i.e., closer the planet to the sun, its time period is less.