Inelastic collision
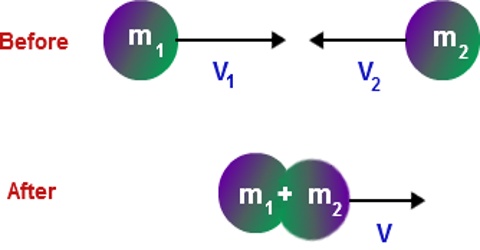
An inelastic collision is a collision in which there is a loss of kinetic energy. While momentum of the system is conserved in an inelastic collision, kinetic energy is not. You just make a collision between two balls made of soft mud. You will see that total kinetic energy does not remain conserved in this collision. This type of collision is also an ideal event. It is an example of inelastic collision. That means, after collision between two bodies if they combine with each other and move as a single body i.e., the relative velocities of the two bodies become zero, then it is called inelastic collision.
In figure, a total inelastic collision has been shown. Here two bodies of masses m1 and m2 moving along the same straight line and in the same direction with velocities v01 and v02 respectively collide with each other. After collision the two bodies combine with each other and start moving in the same direction as a single body with velocity v.
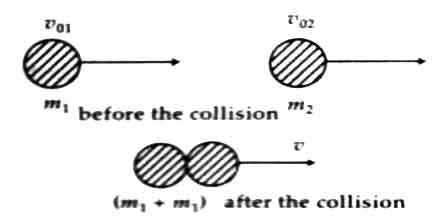
Fig: Total inelastic collision
Example: All ordinary collisions are inelastic in nature because in this collision, the kinetic energy is changed into internal energy; for examples, collision between car, trucks or airlines etc. Two automobiles crash into each other, and the front ends of each crumple up. You bounce a basketball on the ground for a while and notice that it gets warmer and warmer as you bounce it.
Mathematical Explanation: From the principle of conservation of linear momentum, we get,
Total momentum before collision = Total momentum after collision
so, m1v01 + m2v02 = (m1 + m2)v
or, v = (m1v01 + m2v02) / (m1 + m2)
By subtracting the total kinetic energy before collision ½ mv022 + ½ m2v022 from the total kinetic energy after collision ½ (m1 + v2)v2, we can find dissipation of kinetic energy. It is seen that dissipation of kinetic energy is proportional to the square of relative velocity (v01 – v02).