The ideal gas law connects the pressure, volume, and temperature:
(1) for a fixed volume, a higher temperature leads to an increase in pressure, P ≈ T,
(2) at constant pressure, a higher temperature leads to an increase volume, V ≈ T, and
(3) at constant temperature, a higher pressure is associated with a smaller volume, P ≈ 1/V. This can be summarized as
PV / T = const,
where T is the absolute temperature [measured in Kelvin]. This law assume that the amount of gas [i.e., the mass] is kept constant.
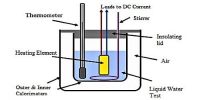
Example: A glass column is filled with air. At room temperature, the pressue is 2.5-times the atmospheric pressure. What is the pressure inside the glass column when it immersed in boiling water?
Solution:
We have the absolute temperatures T0 = 298 K and Tf = 373 K.
Since the volume is constant V0 = V1 = V, P0 V / T0 = P1 V / T, so that,
P1 = (T1/T0) P0 = (373K/298K) 2.5atm = 3.1 atm
In an ideal gas, molecules are moving in random directions aat random speeds inside a container. The molecules bounce off the walls. During a collision, the wall of the container exerts a force on a molecule; thus, the molecule exerts a (reaction) force on the container wall: the summation of all forces from all collisions produces the macroscopic pressure.
A simplified derivation starts from a cubic container with volume V = L3 ; we we choose a coordinate system aligned with the cube. We assume that the molecule travels with speed v along the x -coordinate. The collision with the wall gives the change in momentum Δp = (-mvx) – m(vx) = – 2mvx, . Since the time between consecutive collisons is t = 2L/v , the (average) force by one molecule follows Faye = ( -2mvx)/ (2 L/vx) = – mvx2/L . The particle moves in all directions so that vx2 = (v2) /3, where we introduced the mean square value (v2) . Thus for the force due to N molecules F = Nm (v2) /3L so that for the pressure P = F/L2 = Nm (v2) /3V.
We find,
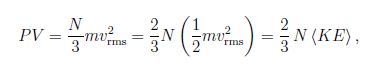
where we introduced the average kinetic energy of the molecule (KE) = m (v2) /2. Comparison with ideal gas law PV/T = const yields
(KE) = (m/2) V2rms = 3/2 kT,
where k = 1.381 x 10-23 J/K is the Boltzmann constant.
The number of molecules in a gas is enormous N > > 1. Avogardo’s number is used to quantify large numbers,
NA = 6.022 x 1023
The number of moles is then given by n = N/ NA
The product of the molecular mass and Avogadro’s number is the molar mass M = NA m. For helium Mhe ≈ 4 g; and air [80% N2 and 20% O2]. Mair = 28.8 g. Avogadro’s number and the Boltzmann constant are the connection between microscopic and macroscopic quantities. The unit for masses of molecules is the atomic mass unit:
1 u = (1 g / NA) = 1.66 x 10-27 kg. NA