Example 1: At time t = 0, the displacement is x = 2.72 m, the velocity is v = —2.54 m/s, and the acceleration is a = —10.87 m/s2.
a) Find the amplitude, phase, and angular frequency for the harmonic motion.
b) Find expressions for x(t), v(t), and a(t).
Solution: We find for the ratio of the acceleration and coordinate,
a/x = -(10.87 m/s2) / 2.72 m = – 4.0 s-2 = -ω2 → ω = 2.0 s-1
and the period is T = 27π /w = 2π/(2.0s-1) = 3.1 s.

Example 2: Find the period of a mathematical pendulum that is an object with mass in attached to a string of length L.
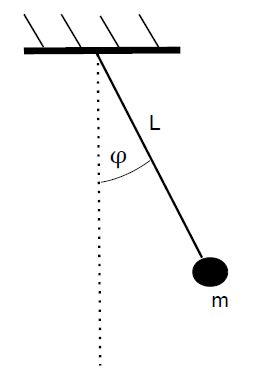
Solution: The force on the object is the weight F = mg (directed downward). For the torque about the fix point on the ‘ceiling: we get
τ = -mg • L sin ϕ.
Note that the torque is negative (clockwise) [positive (counter-clockwise)] when the angular displacement is positive, ϕ > 0 [negative ϕ < 0]. Since the moment of inertia is I = mL2, we have τ = lα, so that -mgL sin α = mL2 sin ϕ , or α = (g/L) ϕ
Then we find yields: T = 2π √(L/g)
Discussion: We find the length of a mathematical pendulum with period T = 2.0 s. We get L = (9.8 m/s2)/ (πs)2 = 1.0m.











