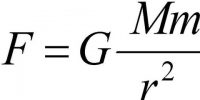Gravitational potential due to a point mass
We know, the amount of work done in bringing a unit mass from infinity to a point in the gravitational field is called the gravitational potential at that point. Now, we need to find the equation of gravitational potential due to a point mass. A potential is a scalar field that describes the potential energy per unit of some quantity due to a vector field.
The equation for gravitational potential energy is:
⇒ GPE = m⋅g⋅h
Where,
m is the mass in kilograms,
g is the acceleration due to gravity (9.8 on Earth)
h is the height above the ground in meters.

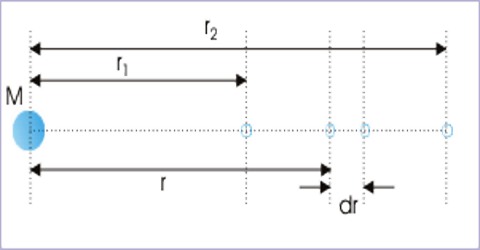
Let an object of mass M be placed at point O [Figure]. P is a point at a distance r from O. The gravitational potential at point P is to be found out. The gravitational potential of a point is equal to the potential energy that a unit mass would have at that point. Under the action of gravitational force, the work done is independent of the path taken for a change in position so the force is a conservative force. Besides, all such forces have some potential in them.
Gravitational Potential of a Point Mass
Consider a point mass M, the gravitational potential at a distance ‘r’ from it is given by;
V = – GM/r.
At point P the attractive force on unit mass in the direction of O i.e., gravitational intensity = GM/r2. Now, the amount of work done i.e., potential in taking the unit mass by a very small distance dr is,
dV = force x displacement = intensity displacement = (Gm/r2) dr
So, Total work done in bringing the unit mass from infinity to point P is,
V = ∫ dV = r=r∫r=∞ (Gm/r2) dr
or, V = GM r=r∫r=∞ (1/r2.dr) = GM [- 1/r]r∞
or, V = – GM/r
Here negative sign indicates that the work has not been done by any external agent; the gravitational force itself has done the work. All conservative forces have potential energy associated with them. The force of gravity is no exception. Gravitational potential energy is usually given the symbol Ug, start subscript, g, end subscript. It represents the potential an object has to do work as a result of being located at a particular position in a gravitational field.
Special cases:
(i) By considering all the masses of a uniform solid sphere of the uniform sphere at their center potential at outside points of those spheres can be found out. The gravitational influence on a body at infinity is zero, therefore, potential energy is zero, which is called a reference point.
(ii) The potential at all points inside a solid sphere remains constant. This potential is equal to the potential at the surface of the sphere. If M is the mass of the sphere and r is the radius then the potential at any point inside the sphere is V = – GM/r.