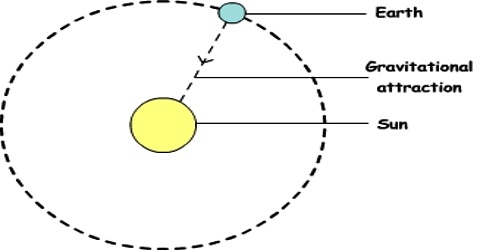
Gravitational force between the sun and the earth:
We know that to determine the gravitational force at a point outside a uniform solid sphere, it is considered that the mass of the sphere is concentrated at its centre. So, in order to find the gravitational force acting between two stars we can consider each star as a particle whose mass is concentrated at the centre. By Newton’s Law of Universal Gravitation, there is the gravitational force between any bodies having mass. Each body attracts another body, and the direction of this force is along the straight line that goes through the bodies.
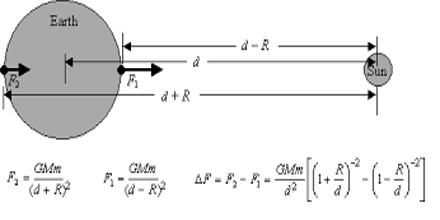
We know,
Mass of the sun, M1 = 1.99 x 1033 g = 1.99 x 1030 kg
Mass of the earth, M2 = 5.96 x 1027 g = 5.96 x 1024 kg
Again, although earth’s orbit is not exactly circular but we consider it to be almost circular.
Average distance between the sun and the earth, d = 1.497 x 1013 cm = 1.497 x 1011 m
So, gravitational force acting between the sun and the earth,
F = [Gm1m2/d2]
= [(6.67 x 10-11) x (1.99 x 1030) x (5.96 x 1024)] / [1.497 x 1011]2
= 3.53 x 1022 N