General Law In Geometrical Addition of Vector Quantities
Of the two vectors, the end or head point of the first vector and the initial point or tail point of the second vector are placed on the same point, then the direction of the straight line connecting the initial or tail point of the first vector and the end or head point of the second vector will give the direction of the resultant vector. The length of that straight line will give the magnitude of the resultant vector.
Suppose two vectors P and Q are acting at the same time at the same point, we need to find out the resultant vector R.
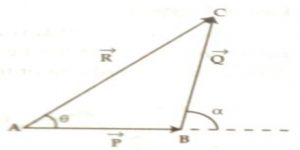
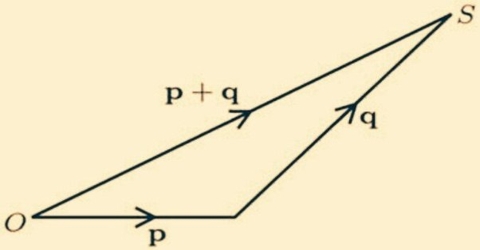
Let the tail point of the vector Q represented by line BC be placed at the head or arrow point of the vector P represented by line AB [Fig. 1]. Now, let us draw the line AC connecting the tail point of P and head point of Q, then the line AC will give the resultant vector R. So, the addition of vectors P and Q is:
R = P + Q … … … (1)
Similarly, more than two vectors can be added.
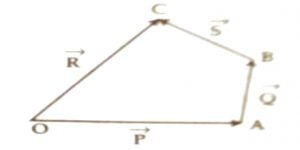
In fig. 2, three vectors P, Q and S have been indicated by straight lines OA, AB, BC and by straight line OC their resultant has been indicated by R.
Here, resultant, R = V + Q + S.