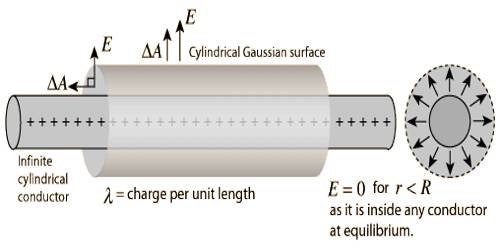
Gauss’s Law to determine Electric field due to charged line of infinite length
The electric field of an infinite line charge with a uniform linear charge density can be obtained by a using Gauss’ law. Let us consider a uniformly charged wire charged line of infinite length whose charge density or charge per unit length is λ. Let a point P at a distance r from the charge line be considered [Figure]. Electric field E at point P is to be determined.
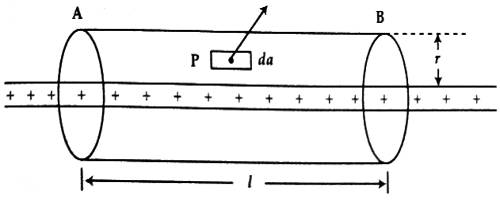
Let us consider a Gaussian cylinder of length ‘l’ and radius ‘r’ taking the charge line as axis. Then the point P will be on the curved surface of the cylinder. The magnitude of the electric field E→ of all points on the curved surface is same and direction is outward along normal to the curved surface. So, at point P electric field E→ and field vector da→ are in the same direction. Hence according to Gauss’s law,
ε0 § E→.d a→ = ε0 §Eda = λl.
or, ε0E§ Eda = λl.
or, ε0E (2πrl)a = λl
So, E = λ/ (2πε0r)
E acts perpendicular to the normal of the two circular surfaces of Gaussian cylinder. Hence, for both the curved surfaces ε0§E→.d a→ = 0. So, the required electric field, E = λ / (2πε0r).