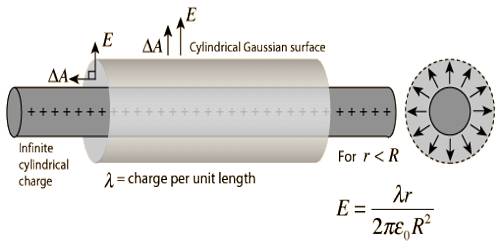
Gauss’s Law to determine Electric field due to charged long cylinder
The electric field of an infinite line charge with a uniform linear charge density can be obtained by a using Gauss’ law. Let us consider a long cylinder of radius ‘r’ charged uniformly. Charge per unit length in it is λ. suppose, an electric field is to determine at a distance r from the axis of the cylinder.
Let us consider a cylinder of radius ‘r’ and length L co-axial with the cylinder. This type of cylinder is called Gaussian cylinder. As the cylinder is very long, hence the influence of its two ends may be ignored. Then due to symmetrical property magnitude of the electric field E→ is equal everywhere in the Gaussian cylinder and the direction will be outward along the radius. The direction of any small surface da→ considered is outward along the radius (Figure). The amount of charge due to the Gaussian surface will be, q = λL.
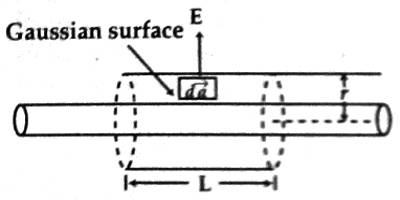
Now, according to Gauss’s law, we get,
∫S E→.d a→ = ∫S Eda = q/ε0
or, E (2πrl) = λL/ε0
E = λ / 2πε0r
It is the required electric field. If expressed in vector form we get,
E→ = (λ / 2πε0) r→/r2