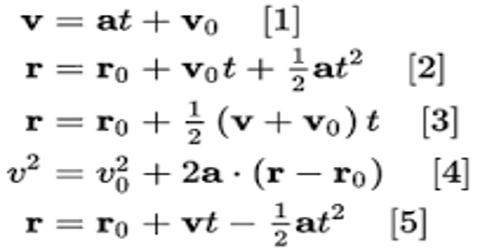Fourth Equation of Dimensional Motion

Fourth Equation

Relation between initial velocity, final velocity and displacement or position

v² = v₀² + 2as or, v_x² = v_x0² + 2a (x – x₀)

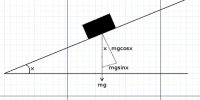
Let an object move at a particular direction with uniform acceleration ‘a’. Let at t = 0 its initial velocity be v₀ and at t = t, the final velocity ‘v’ and during this time interval the displacement of the object is ‘s’. Now, we know,

v = v₀ + at … … … (1)

and s = v₀t + ½ at² … … … (2)

Now squaring both sides of equation (1), we get;

v² = (v₀ + at)² = v₀² + 2 v₀at + a²t²

= v₀² + 2a (v₀t + ½ at²)

= v₀² + 2as [using equation (2)] … … … (3)

For one dimensional notion, say along X-axis let v₀ = v_x0, v = v_x, a = a_x and s = x – x₀, where x₀ is the initial position at t = 0 and x the final position at t = t. Then from equation (3) we get;

v_x² = v_x0² + 2a_x + 2a_x (x – x₀)