The density of an object is defined as the ratio of mass in divided by its volume,
P = m/V
The unit of density is [p] = [m]/[V] = kg/m3. The density of liquids and solids are of the order of thousands of kilograms per cubic meter [p ≈ 103 kg/m3] and is about a thousand times smaller [p ≈ 1 kg/m3] for gases, which is consistent with the times greater distance between atoms (molecules). For H2O, the respective densities are:
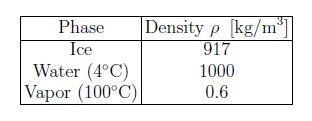
H2O is has many unusual properties: among them is the greater density in the liquid phase compared to the solid phase. Note that the density of vapor strongly depends on temperature and pressure [see below].
Example: The approximate density of the human body is close to that of (liquid) water p ≈ 1000 kg/m3. Find the volume of a person.
Solution: For m = 70 kg [or 155 lbs], so for the volume,
V = M/P = (70 kg / 100 kg/m3) = 7.0 x 10-2 m3 = 7.0 x 104 cm3.
This is equivalent to the volume of a cube with length a ≈ 41 cm.
The response [e.g., the deformation] of a system to an external force F also depends on the size of the system. Pressure is defined as the ratio of force divided by the area,
P = F/A
The SI unit of pressure is [P] = [F]/[,11] = N/rn2 = Pa [“Pascal”]. Normal atmospheric pressure is Patm = 1.015 x 105 Pa. Pressure explains why we sleep in beds rather than on the floor. the forces exerted by the mattress and the floor on the person are equal [and equal to the weight of the person]. A mattress adjusts its shape to the person’s body, thereby increasing the area and decreasing the pressure.
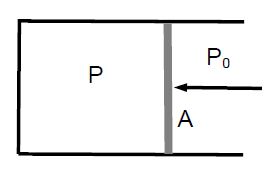
The pressure inside and outside a piston is P and P0 < P, respectively. If the cross-sectional area of the piston is A, a force F = (P – P0) • A must be applied to move the piston to the left.
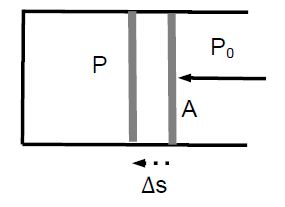
If the piston is displaced by Δs, work is done on the gas: W=F•As. We find W = F Δs. We find W = PA*Δs) = P(A*Δs) = – P ΔV, where we used A Δs = -Δs [negative, because the volume of the gas decreases]. This yields an alternative definition of pressure
P = – (W / ΔV)
which is useful in many applications, especially when the change in the volume ΔV is small and the change in pressure can be ignored.
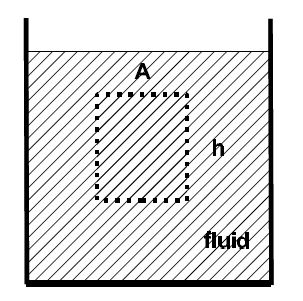
We examine the effect of gravity on a fluid. We consider a fluid element with a cross-sectional area A and a height h. The forces on the element are from the top Ft, the bottom Fb, the left Fl, and the right Fr.
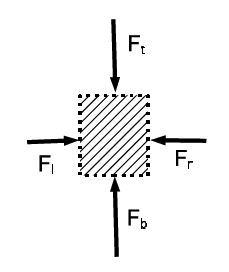
There is no difference between left and right [since we cannot differentiate between the volume element and its mirror image] so that Fl = Fr. Since the volume element is in mechanical equilibrium, the difference between the force from the bottom and top is equal to the weight: Fb – Ft = mg. This difference is produced by the pressure difference Fb — Ft = (Pb — Pt)A. The mass of the element is m = pV = pAh . We get (Pb — Pt)A = pAhg , or (P — Pt) = pgh . If P0 is the pressure on top of the surface, the pressure at the distance h below the surface is:
P = P0 + pgh.
That is, the pressure increases with the depth below the surface of fluid at rest: hydrostatic pressure.