Interference of light:
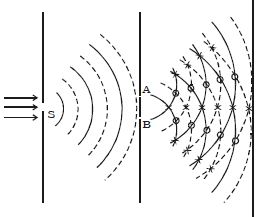
Two slits A and B illuminated by a single monochromatic source S act as coherent sources. The waves from these two coherent sources travel in the same medium and superpose at various points as shown in Figure. The crest of the wavetrains are shown by thick continuous lines and troughs are shown by broken lines. At points where the crest of one wave meets the crest of the other wave or the trough of one wave meets the trough of the other wave, the waves are in phase, the displacement is maximum and these points appear bright. These points are marked by crosses (x). This type of interference is said to be constructive interference.
Fig: Interference phenomenon
At points where the crest of one wave meets the trough of the other wave, the waves are in opposite phase, the displacement is minimum and these points appear dark. These points are marked by circles (O). This type of interference is said to be destructive interference. Therefore, on a screen XY the intensity of light will be alternatively maximum and minimum i.e. bright and dark bands which are referred as interference fringes. The redistribution of intensity of light on account of the superposition of two waves is called interference.
The intensity of light (I) at a point due to a wave of amplitude (a) is given by I ∝ a2.
If a1 and a2 are the amplitude of the two interfering waves, then
I1 ∝ a12 and I2 ∝ a22
so, I1/I2 = a12/ a22
For constructive interference, Imax ∝ (a1 + a2)2 and for destructive interference, Imin ∝ (a1 – a2)2
Imax/ Imin = (a1 + a2)2/ Imin ∝ (a1 – a2)2