Explain Magnification for Real and Virtual Image

Let consider an object OO’ placed on the principal axis with its height perpendicular to the principal axis as shown in Figure. The ray OP passing through the optic centre will go undefeated. The ray O’A parallel to the principal axis must pass through the focus F₂. The image is formed where O’ PI’ and AF₂I’ intersect. Draw a perpendicular from I’ to the principal axis. This perpendicular II’ is the image of OO’.

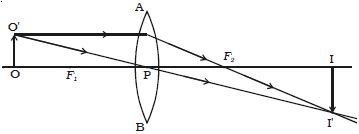
The linear or transverse magnification is defined as the ratio of the size of the image to that of the object.

.-. Magnification m = [Size of the image/Size of the object] = II’/ OO’ = h₂/h₁

where h₁ is the height of the object and h₂ is the height of the image.

From the similar right angled triangles OO’ P and II’ P, we have; II’/OO’ = PI/PO

Appling sign convention;

II’ = – h₂; OO’ = + h₁

PI = + v; PO = – u

Substituting this in the above equation, we get magnification,

M = [-h₂ / +h₁] = [+v/-u]

so, m = + (v/u)

The magnification is negative for real image and positive for virtual image. In the case of a concave lens, it is always positive.