(A) Point object
In figure (1), O is an object in front of a plane mirror M1M2. Ray OT from the point 0 incident normally on the plane mirror and reflected back along TO. Another ray OQ incident obliquely on the mirror and reflected along the path QR. If the reflected rays QR and TO are extended backward, they meet at the point I. As if the reflected rays are coming from the point I situated behind the mirror. Therefore, the point I is the virtual image of the point O.
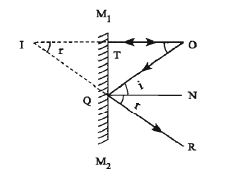
The normal QN is drawn at the point Q.
Since TO and QN are parallel, OQ is the interjector.
So, ˄TOQ = ˄OQN = I …… …….. ……(1)
Again, OI and QN are parallel, line RQI has intersected them.
So, ˄TIQ = ˄NQR = r …… …… ……… (2)
We know, i = r
We get from equations (1) and (2), ˄TOQ = ˄TIQ
Now between ˄QOT and ˄Q1T,
˄TOQ = ˄T1Q, TQ is a common arm,
and ˄QT0 = ˄QTI = 90°
Therefore, the triangles are equal in all respects.
Hence, OT = TI
The image I in a plane mirror is at the same distance behind the mirror as the object O is in front.
(B) Extended object
The image of an extended object can also be drawn as the point object. In this case, the extended object should be considered as an aggregation of infinite number of points. Here, a virtual image is formed for each point behind the mirror [Figure 2].
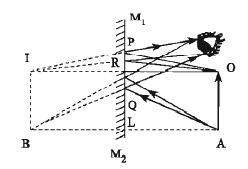
In the figure an object AO and its image BI are shown. From the points 0 and A, perpendiculars are drawn on the mirror M1M2. They intersect the mirror at the points R and L. Now OR and AL are extended backward to the points I and B respectively, such that OR=IR and AL=BL. Two rays from each of the points 0 and A incident obliquely on the mirror and get reflected. When the two reflected rays are produced backward, they seem to be coming from the points I and B respectively. Now I and B are joined. Therefore, BI is the virtual image of the object AO formed in the plane mirror.
The size of the image formed in a plane mirror is always equal to that of the object.
The characteristics of the image formed in a plane mirror.
The images formed by a plane mirror have the following properties:
- The image in a plane mirror is at the same distance as the object is in front.
- The size of the image is equal to the size of the object
- The image is virtual and erect.