In 1738, Daniel Bernoulli proposed a theorem for the streamline flow of a liquid based on the law of conservation of energy. According to Bernoulli’s theorem, for the streamline flow of a non-viscous and in compressible liquid, the sum of the pressure energy, kinetic energy and potential energy per unit mass is a constant.
P/ρ + v2/2 + gh = constant
This equation is known as Bernoulli’s equation.
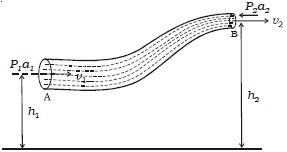
Consider streamline flow of a liquid of density ρ through a pipe AB of varying cross section. Let P1 and P2 be the pressures and a1 and a2, the cross sectional areas at A and B respectively. The liquid enters A normally with a velocity v1 and leaves B normally with a velocity v2. The liquid is accelerated against the force of gravity while flowing from A to B, because the height of B is greater than that of A from the ground level. Therefore P1 is greater than P2. This is maintained by an external force.