Isaac Newton created his revolutionary Law of Cooling in the 17th century. Newton s law of cooling states that the rate of cooling of a body is directly proportional to the temperature difference between the body and the surroundings. Newton’s Law of Cooling is a formula that allows us to determine the temperature of an object during heat loss.
Let consider a spherical calorimeter of mass m whose outer surface is blackened. It is filled with hot water of mass m1. The calorimeter with a thermometer is suspended from a stand (Fig).
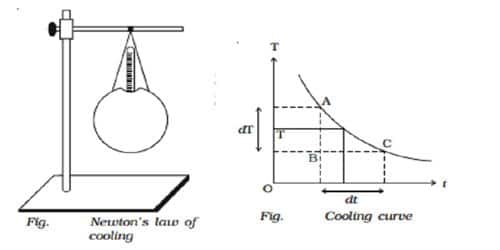
The calorimeter and the hot water radiate heat energy to the surroundings. Using a stopped clock, the temperature is noted for every 30 seconds interval of time till the temperature falls by about 20° C. The readings are entered in a tabular column.
Isaac Newton stated that ¨the rate at which a warm body cools is proportional to the difference between the temperature of the warm body and the temperature of its environment.¨ Newton’s theory can also be put into an equation, giving us the Law of Cooling equation:
T (t) = TS (T0 – TS) e-kt
With T (t) being the temperature of an object at a certain time
t being the time in seconds
Ts is the temperature of the surroundings
T0 is the starting temperature of the object
and k being the cooling constant.
If the temperature of the calorimeter and the waterfalls from T1 to T2 in t seconds, the quantity of heat energy lost by radiation Q = (ms + m1s1) (T1 – T2), where s is the specific heat capacity of the material of the calorimeter s1 is the specific heat capacity of water.
The rate of cooling = Heat energy lost / time taken
so, Q/t = (ms + m1s1)(T1 – T2) / t
If the room temperature is T0, the average excess temperature of the calorimeter over that of the surroundings is [{(T1 + T2)/2) – T0]
According to Newton’s Law of Cooling, Q/t α [{(T1 + T2)/2) – T0]
[Q/t = (ms + m1s1)(T1 – T2) / t] α [{(T1 + T2)/2) – T0]
so, [(ms + m1s1)(T1 – T2)] / [t.{(T1 + T2)/2 – T0}] = Constant
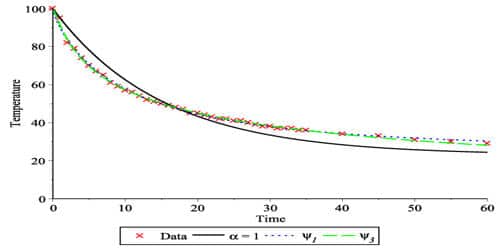
The time for every 4° fall in temperature is noted. The last column in the tabular column is found to be the same. This proves Newton’s Law of cooling. Using this equation, we can calculate how fast an object at a certain temperature would cool in a specific environment, and how the rate of cooling of an object is dependent on the difference of temperature between the object and the surroundings but also on the cooling constant of the object.
The law holds good only for a small difference in temperature. The loss of heat by radiation depends on the nature of the surface and the area of the exposed surface. It is relatively easy to experimentally verify Newton’s Law of Cooling. After calculating the rate of the cooling curve, we find that the rate of cooling is proportional to the difference between the temperature of the object and the temperature of the surroundings, verifying Newton’s Law of Cooling.