Experiment: Determination of Young’s Modulus
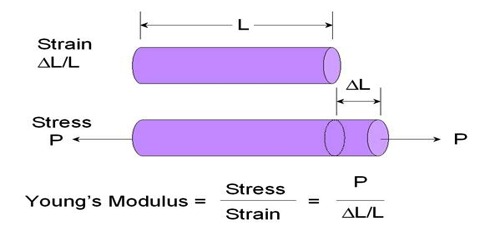
Theory: Young’s modulus means the ratio of longitudinal stress and longitudinal strain within elastic limit. It is denoted by Y.
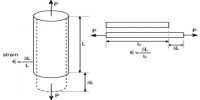
If at the lower end of wire of length ‘L’ and cross-sectional area of ‘A’ a load of ‘m’ is pressed and if the length increases by l, then;
Longitudinal stress = F/A = mg/A [here, g = acceleration due to gravity]
and, Longitudinal strain = l/L
Longitudinal stress, Y = [Longitudinal stress / Longitudinal strain] = (F/A) / (L/l)
or, Y = (mg/A) / (l/L) = mgL/Al
If applied force and cross-sectional area and length are expressed in C.G.S unit, then Y = (mgL/Al) dyne/cm2.
Apparatus: (1) vernier instrument, (2) metre scale (3) screw gauge and (4 necessary weights.
Procedure:
(1) Firstly, determine the vernier constant of the instrument. Then by applying a load in the experimental wire it is made straight. This step can be applied in the reference wire as well. This bad is called dead load. Finally, a reading of the main with the help of vernier scale is taken.
(2) Diameters of the experimental wire at different points are measured by a screw gauge and the average value of diameter is found out. This diameter is divided by 2 and radius r of the wire is noted and area of cross-section A = πr2 is determined.
(3) By multiplying the breaking stress of the experimental wire by the area of cross-section of the wire breaking weight is found out.
(4) Length of the experimental wire from the point of suspension to 0 mark in the vernier is measured by a metre scale. Let the initial length of the wire be L.
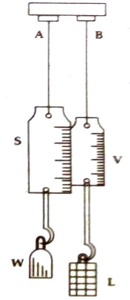
(5) Now by putting ½ or 1 kg weight in the hook of the wire length of the wire is measured from the main scale and the vernier scale.
(6) In this way weights are put on the wire in succession, increase of length is found out in each case from the main scale and vernier scale. (It must be noticed that applied load does not exceed half of the value of breaking weight). In every case, by subtracting from the original length increase of length of the wire is found out for the applied load.
(7) In this way by increasing and later on by decreasing loads in succession readings are taken from the main scale and vernier scale.
(8) Then for each load average value of expansion and contraction of the wire for each load is found out. Thus value l is inserted in the equation and Young’s modulus found out.
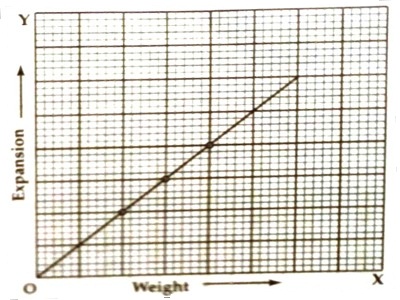
(9) Sometimes, a graph is plotted by a load in the X-axis and the related expansion in the Y-axis. This graph will be a straight line passing through the origin. This straight line proves the Hooke’s law. From the straight line perpendicular lines from a particular point is drawn on the X and Y-axes. By knowing the weight and expansion from the intersections on the axes, Young’s modulus is determined from the equation, Y = mgL/πr2l