Experiment: Determination of the Spring Constant
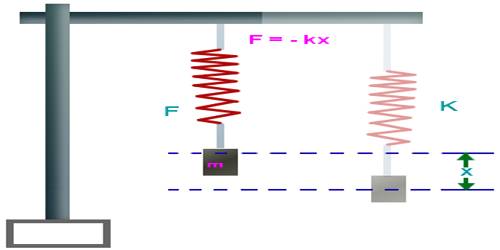
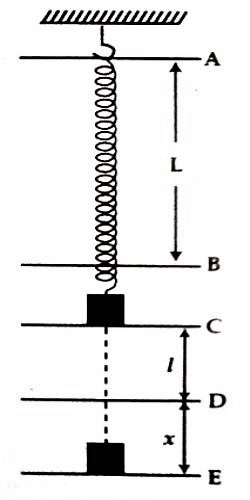
Theory: If a mass ‘m’ is hanged from the end of a vertically hanged spiral spring, then the length of the spring increases by length ‘l’. In this situation, the body is assumed to be at equilibrium. Now, the body is pulled by a .distance x downward and is released, then it will execute simple harmonic motion [Figure].
During pulling the body downward a restoring force acts along the initial position of the spring. According to Hooke’s law, this restoring force is proportional to ‘x’ and oppositely directed. So,
F = – K/x
Here K is the force constant of the spring. If the body is released after pulling, it moves with acceleration a due to the force F. If the mass of the body is ‘m’ its acceleration will be,
a = F/m = – (Kꞌ/m)x
So, a = – Kx … … … (1)
Here, K = (Kꞌ/m)x = constant = spring constant.
So, the motion of the body will be simple harmonic motion.
Since for unit displacement, acceleration = Kꞌ/m
So, time period of the oscillating body, T = 2π √(m/K) … …. ….. (2)
Due to the action of the weight mg of the body the spring is elongated by length ‘l’, so, according to Hooke’s law, mg = Kl.
or, K = (m/l) g … … …. (3)
or, m/K = l/g
So, Time period of the oscillating body, T = 2π √(l/g) … … … (4)
Equipments: (1) Experimental spring, (2) Some convenient weights, (3) A hook to suspend the spring, (4) Meter scale.
Procedure:
(i) Suspend the spring from the end of the experimental table or from a rigid may.
(ii) Measure the length L of the spring by a meter scale.
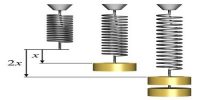
(iii) Now a weight is hanged at the end on the spring, consequently the spring is elongated and it clench from C to D. This increase in length is measured by a meter scale. A mark is to be given along the point D.
(iv) Above procedures are followed a times with different weights and increase in length ‘l’ is measured for different weight.
Drawing of a graph: On the graph paper by putting weight along X-axis and increase in length 1 along Y-axis a graph is drawn. The graph becomes a straight line passing through the origin O (Figure 2). The Slope of this straight line l/m is determined.
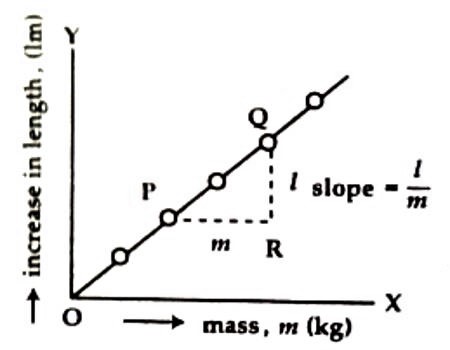
Calculation: m/l is found out from the experimental value l/m and by inserting the value of ‘g’ in equation (3) the spring constant is determined.
Result: The value of the spring constant is … … N/in.
Discussion and precautions:
(1) The spring is to be hanged in such a way that after hanging a weight at its end, the upper end of the hook does not come out from the spring.
(2) Find the elongation of the spring for the increase of weight.
(3) Care should be taken so that while hanging weight on the spring there should not be any resistance for increase in length.
(4) Elongation should be measured carefully.