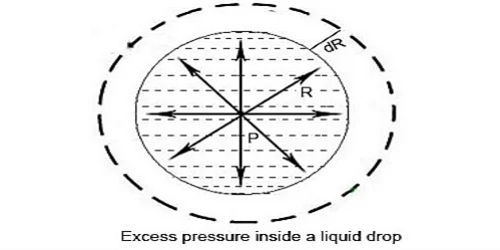
Consider a liquid drop of radius r, and surface tension T. The molecules on the surface of the drop experience a resultant force acting inwards due to surface tension. Due to surface tension the molecules on the surface film incident the net energy in the inward course normal to the surface. Therefore, the pressure inside the drop must be greater than the pressure outside it. The pressure inside the liquid drop must be greater than the pressure outside as the size of the drop cannot be reduced to zero. The excess of pressure P inside the drop provides a force acting outwards perpendicular to the surface, to balance the resultant force due to surface tension. Therefore there is more force inside than outside. Imagine the drop to be divided into two equal halves. Due to the surplus of pressure surrounded by the liquid drop the free surface of the drop will occurrence the net force in external direction due to which the drop will enlarge. This excess pressure inside the drop provides a force outwards, vertical to the surface to counter equilibrium the resultant force due to the surface tension.
It is because of surface tension that the force of a liquid increase within a bubble.
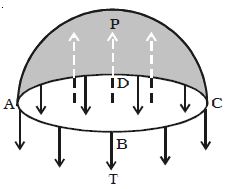
Considering the equilibrium of the upper hemisphere of the drop, the upward force on the plane face ABCD due to excess pressure P is P π r2 (Figure).
If T is the surface tension of the liquid, the force due to surface tension acting downward along the circumference of the circle ABCD is T 2πr.
At equilibrium, P πr2 = T2πr
P = 2T/r