Equation of motion of a horizontal projectile
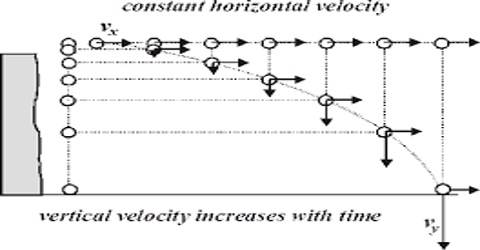
Let an object be thrown from a point O with velocity v0 along the horizontal direction [Figure]. If we ignore air resistance and consider g constant, then along the path of motion of the thrown object v0 will remain constant. Let after t sec the object reach at point P travelling distances x and y, respectively along horizontal and vertical directions. Now let the velocity at P be v. The horizontal and vertical components of v are respectively vx and vy.
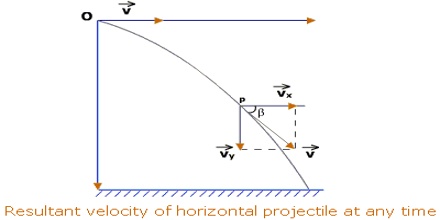
So, vx = v0 = v cos θ
and vy = v0 + gt = 0 + gt = v + sin θ
[as we know, v0 = 0 along vertical direction]
so, v = √(vx2 + vy2)
here angle θ in between v and horizontal direction, i.e., along X-asis,
and, tan θ = vy/vx
Again, x = v0 + t … … … (1)
[ax = 0 along horizontal direction]
so, t = x/v0
and, y = ½ gt2 …. …. …. (2)
[v0 = 0 along vertical direction]
Now, inserting the value of t from equation (1) in equation (2) we get,
y = ½ g(x/v0)2
so, x2 = (2v02/g).y … … … (3)
Since, v0 and g are constant, if we put 2v02/g = 4A, we get,
x2 = 4A.y
This is an equation of parabola. So, trajectory of a body or a projectile ejected horizontally in resistant free-path forms a parabola.