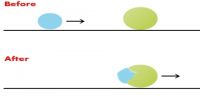
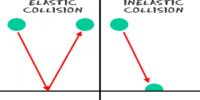
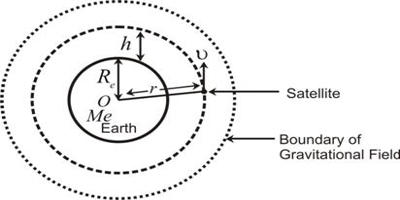
A satellite revolving in a circular orbit round the Earth possesses both potential energy and kinetic energy. If h is the height of the satellite above the Earth’s surface and R is the radius of the Earth, then the radius of the orbit of satellite is r = R + h.
If m is the mass of the satellite, its potential energy is,
EP = -GMm/r = -GMm/(R+h)
Where M is the mass of the earth. The satellite moves with an orbital velocity of, v0 = √GM/(R+h)
The total energy of the satellite is, E = EP + EK
E = – GMm/2(R+h)
The negative value of the total energy indicates that the satellite is bound to the Earth.