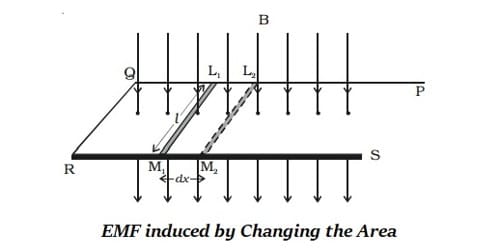
Emf Induced by Changing the Orientation of the Coil
The magnetic induction can be changed by moving a magnet either towards or away from a coil and thus an induced emf (electromotive force) is produced in the coil.
Let consider, PQRS is a rectangular coil of N turns and area A placed in a uniform magnetic field B (Figure). The coil is rotated with an angular velocity ω in the clockwise direction about an axis perpendicular to the direction of the magnetic field. Suppose, initially the coil is in a vertical position so that the angle between normal to the plane of the coil and magnetic field is zero. Motion in a magnetic field that is stationary relative to the Earth induces motional EMF. Any transform in magnetic flux induces an EMF opposing that alter, a procedure known as induction. Motion is one of the key causes of induction.
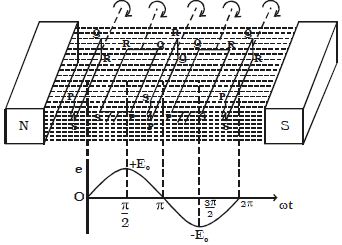
Fig: Induced emf by changing the orientation of the coil
After a time t, let θ (=ωt) be the angle through which the coil is rotated. If φ is the flux linked with the coil at this instant, then φ = NBA cos θ
The induced emf is,
e = – dφ/dt = − NBA d/dt cos (ωt)
∴ e = NBAω sin ωt … … (1)
The maximum value of the induced emf is, E0 = NABω
Hence, the induced emf can be represented as e = E0 sin ωt The induced emf e varies sinusoidally with time t and the frequency being ν cycles per second (v = ω/2π)
(i) When ωt = 0, the plane of the coil is perpendicular to the field B and hence e = 0.
(ii) When ωt = π/2, the plane of the coil is parallel to B and hence e = E0
(iii) When ωt = π, the plane of the coil is at a right angle to B and hence e = 0.
(iv) When ωt = 3π/2, the plane of the coil is again parallel to B and the induced emf is e = −E0.
(v) When ωt = 2π, the plane of the coil is again perpendicular to B and hence e = 0.
If the ends of the coil are connected to an external circuit through a resistance R, current flows through the circuit, which is also sinusoidal in nature.
The magnetic induction can also be changed in one coil by changing the current in the neighboring coil thus producing an induced emf. If the coil is rotating in a uniform magnetic field, an EMF will be induced if the magnetic flux through the coil is changing.