Experiment: Determination of the radius of curvature of a spherical surface by a spherometer.
Theory: Radius of the curvature which is the portion of a sphere is called the radius of curvature of the spherical surface. It is expressed as R.
Radius of curvature, 6 R = (d2/6h + h/2)
Here, d = Average distance of the three legs of the spherometer;
And h = height or depth of the spherical surface from the surface of the three legs.
Reading of the spherometer = Main scale reading + circular scale reading x least count.
The distance from the center of a round or sphere to its surface is its radius. For other curved lines or surfaces, the radius of curvature at a given point is the radius of a circle that scientifically best fits the curve at that point.
Apparatus: (1) spherometer, (2) plane plate or a big size plane glass slab, (3) spherical surface, (4) meter scale, (5) convex surface (it may be an unpolished convex mirror), (6) mirror, etc.
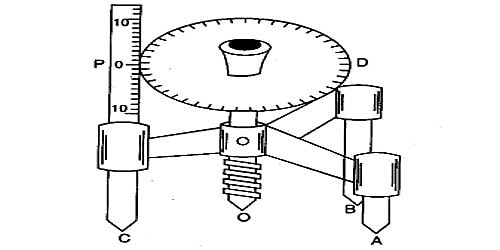
Spherometer ant its parts
A Spherometer is an instrument for measuring the curvature of a surface. For example, it can be used to determine the width of a microscope slide or the depth of depression in a slide. The curvature of a ball can also be measured by using a Spherometer.

A spherometer consists of a metallic tripod structure supported on three fixed legs of equivalent lengths. A screw passes through the center of the tripod frame, parallel to the three legs. A large circular disc graduated with 100 equal parts is attached to the top of the screw.
Procedure:
(1) Find out the pitch and least count of the spherometer by knowing the total number of divisions of the circular scale and value of the smallest division of the spherometer.
(2) Instrumental error, if there is any, is also found out.
(3) The spherometer is placed on a plane plate. The head of the screw is turned in such a way that its end touches the plane plate.
(4) Readings of the linear and circular scales are taken. Vernier or fractional part is found out by multiplying the circular scale reading with least count. Total reading is calculated by adding the linear scale reading and the fractional portion.
(5) Several readings are taken following the above procedures and mean value is found out.
(6) Now place the spherometer on the curved surface. The screw-head is raised slowly and is placed in such a way that its front-end touches the maximum/minimum point of the curved surface. Following the above procedure, the linear scale and circular scale readings are taken and the mean value is found out. Repeating the above procedure a few numbers of readings are taken and the average value is calculated.
The difference between these two readings gives the value h.
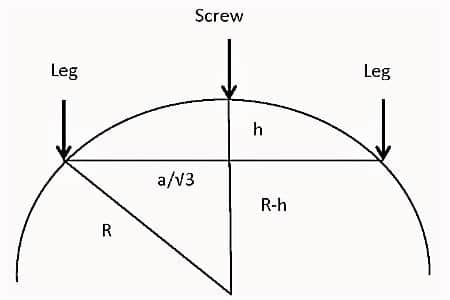
Fig: view of the lens and spherometer from the side
(7) Using the meter scale distances between the three legs are found out and the mean value is calculated. This gives the value of d.
(8) Now using the values of h and d in the above equation R is found out.
Determination of Least count
- Value of the minimum division of the linear scale = x mm
- Pitch = x mm
- Total number of divisions of the circular scale = y
- Least count, K = Pitch/Total no. of circular division = (x/y) mm = … mm
- Distance between the three legs of the spherometer = d mm.
Precautions
- The screw should move freely without friction.
- The screw should be moved in the same direction to avoid the back-lash error of the screw.
- Excess rotation should be avoided.
Sources of error
- The screw may have friction.
- The spherometer may have a back-lash error.
- Circular (disc) scale divisions may not be of equal size.