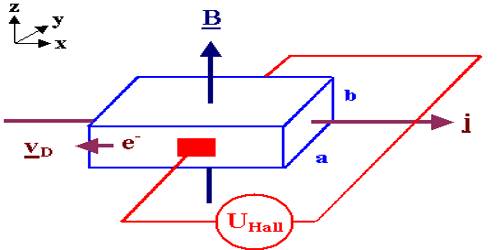
Determination of nature of charges and number of charges in unit volume by Hall potential or Hall voltage.
If a magnetic field is applied perpendicular to the flow of current, then a potential is created normal to both that of current and the magnetic field. This effect is called Hall Effect and the generated potential is called Hall potential or Hall voltage.
Determination of the nature of charges
From the experiment described above, it is seen that it the flow of current is due to the positive charges then along the width of the stripping potential of the upper face (Vu) is higher than the potential of the lower face (Vl), i.e.,
Vul = (Vu – Vl) = positive.
On the other hand, if the flow is due to the negative charges opposite phenomenon will happen. That means, the potential of the lower face Vl will be higher than the potential of the upper face Vu i.e., (Vu ˂ Vl)
So, Vul = (Vu – Vl) = negative.
From this, we can determine the nature of charges.
Determination of the number of charges in unit volume:
Let, q = charge of each carrier
v = velocity of the charges
n = number of charges in unit volume
B = magnetic induction or flux density
E = electric field generated due to the creation of the Hall voltage between the two faces.
VH = Hall voltage
d = Width of the strip.
So, electric field, E = VH/d
or, VH = Ed
Electric force acting on each charge, Fe = qE.
By performing proper calculation it is seen that for Hall potential number of charge per unit volume, n = JB/qE. …. …. …. (1)
here, J = current density = nqb and E = vB
From equation (1) number of charges in unit volume can be determined.
Since velocity of electron, magnitude of the magnetic field, widths of the conductor, electric charge are constant, so mathematically the value of Hall voltage is obtained as-
VH = BI/nqb
This is the equation of the Hall voltage.
Here, B, I, b, d are constants, so VH ∞ 1/n. That means Hall voltage is inversely proportional to the charge density per unit volume.
Note that the direction of the current I in the diagram is that of conventional current so that the motion of electrons is in the opposite direction. That further confuses all the “right-hand rule” manipulations you have to go through to get the direction of the forces.