Metre bridge is one form of Wheatstone’s bridge. It consists of thick strips of copper, of negligible resistance, fixed to a wooden board.
There are two gaps G1 and G2 between these strips. A uniform manganin wire AC of length one metre whose temperature coefficient is low is stretched along a metre scale and its ends are soldered to two copper strips. An unknown resistance P is connected to the gap G1 and a standard resistance Q is connected in the gap G2 (Figure). A metal jockey J is connected to B through a galvanometer (G) and a high resistance (HR) and it can make contact at any point on the wire AC. Across the two ends of the wire, a Leclanche cell and a key are connected.
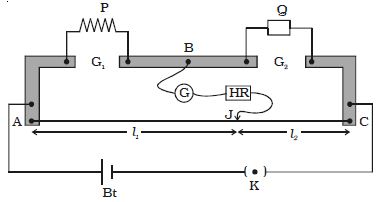
Fig: Metre bridge
Adjust the position of a metal jockey on metre bridge wire so that the galvanometer shows zero deflection. Let the point be J. The portions AJ and JC of the wire now replace the resistances R and S of Wheatstone’s bridge. Then
P/Q = R/S = r AJ / r JC
where r is the resistance per unit length of the wire.
so, P/Q = AJ/JC = l1 / l2
where AJ = l1 and JC = l2
so, P = Q (l1 / l2)
Though the connections between the resistances are made by thick copper strips of negligible resistance, and the wire AC is also soldered to such strips a small error will occur in the value of (l1 / l2) due to the end resistance. This error can be eliminated, if another set of readings are taken with P and Q interchanged and the average value of P is found, provided the balance point J is near the midpoint of the wire AC.