Current loop as a magnetic dipole:
Ampere found that the distribution of magnetic lines of force around a finite current carrying solenoid is similar to that produced by a bar magnet. This is evident from the fact that a compass needle, when moved around these two bodies, show similar deflections. After noting the close resemblance between these two, Ampere demonstrated that a simple current loop behaves like a bar magnet and put forward that all the magnetic phenomena are due to circulating electric current. This is Ampere’s hypothesis.
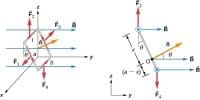
The magnetic induction at a point along the axis of a circular coil carrying current is
B = [μ0 nLa2 / 2(a2+x2)3/2]
The direction of this magnetic field is along the axis and is given by right-hand rule. For points which are far away from the centre of the coil, x>>a, a2 is small and it is neglected. Hence for such points,
B = B = [μ0 nLa2 / 3x3]
If we consider a circular loop, n = 1, its area A = π a2
B = [μ0IA/2πx3] … … (1)
The magnetic induction at a point along the axial line of a short bar magnet is
B = (μ0/4π). (2M/x3)
so, B = (μ0/2π). (M/x3) … … (2)
Comparing equations (1) and (2), we find that
M = IA … … (3)
Hence a current loop is equivalent to a magnetic dipole of moment M = IA
The magnetic moment of a current loop is defined as the product of the current and the loop area. Its direction is perpendicular to the plane of the loop.