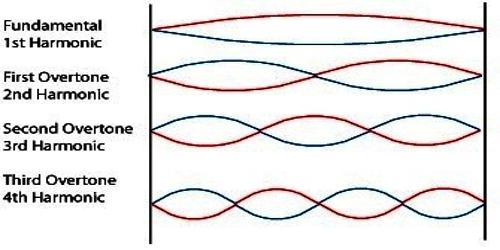
Condition for propagation of Stationary Waves
Stationary waves can form under a variety of conditions, but they are easily demonstrated in a medium which is finite or bounded. It can be produced for both transverse and longitudinal waves. If two ends of a string are fastened straight and if, at a point, is pulled perpendicular to the length, and released, then transverse wave will be generated in the string. This wave after reflecting at the two closed ends will come back and superpose with the principal wave. After some time these two waves will also stop. This type of wave is called stationary wave.
Stationary waves are produced on the following condition:
(1) Two identical waves travelling opposite to each other are needed to superimpose on each other.
(2) The two waves are needed to approach each other with the same speed.
(3) Wave surface contracts in horizontal position.
(4) Wave crest expands in wave position.
(5) At each point displacement of the two waves must be equal and opposite.
(6) Amplitudes of the two waves must be same.
(7) Wavelengths of the two waves must be same.
(8) The reflected wave has to have the same amplitude and frequency as the incoming wave.
(9) The losses of energy at the reflecting surfaces and elsewhere can be made up by the energy supplied by a driver eg. a bow, musician blowing air, etc and this will maintain the stationary wave.