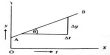
Example: Two people with masses m1 = 45.1 kg and m2 = 65.2 kg are standing on the left and right side of a 4.2 m -long massless raft, as shown. The person on the left holds a ball with mass mb = 7.4 kg.
a) Find the center of mass of the system.
b) The person with mass mi throws the ball to the person with mass mb. Find the displacement of the raft after the second person has caught the ball.
Solution: We have for the total mass Mtot = m1 + m2 + mb = 45.1 kg + 65.2 kg + 7.4 kg = 117.7 kg.
We choose x = 0 at the left side of the boat,
Mtot xCoM = (45.1 kg + 7.4 kg) • 0 + 65.2 kg • 4.2 m = 273.8 kg • m,
so that for the center of mass,
xCM = (273.8 kg • m / 117.7 kg) = 2.33 m
We use Δx for the displacement of the boat. Then
Mtot xCoM = m1 + Δx + (m2 + mb) × (4.2 m + Δx) = Mtot Δx + 304.9 kg • m.
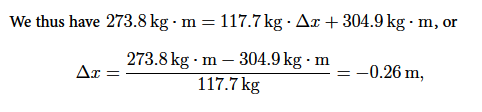
or Δx = —26 cm. That is, the raft is moving towards the left.
Discussion: The person ml exerts a force on the ball directed towards the right. The ball exerts a reaction force on the person towards the left. Note that the conservation of momentum does not tell us the duration of the collision, i.e., the time for the boat to move to its new position.