Application of Newton’s Laws of Motion
When a body applies force on another body then the second body also applies equal and opposite force on the first body. We have learned about this action and reaction forces from Newton’s third law of motion. In nature forces act in couples. In nature, there is not an individual separate force. Two forces are complementary to each other. One of these forces is called action force and the other one is reaction force. As long as action force is there, there exists reaction force also. Practical application of Newton’s laws of motion is described below with an example.
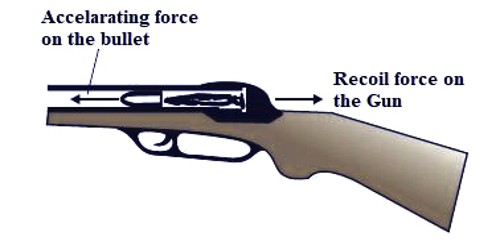
Firing of a bullet from a gun: When a bullet is fired from a gun, the bullet moves ahead with tremendous speed. If the gun applies force F on the bullet, the bullet also applies equal and opposite force on the gun. Due to this reaction force, the gun also recoils backward [Figure].
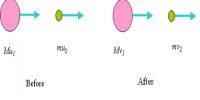
Before the gun is fired, everything is at rest. When a bullet is fired from a gun, the gun exerts a force on the bullet in the forward direction. This is the action force. The bullet experiences a transform in momentum that must be matched by a change in momentum of the gun. The bullet also exerts an equivalent force on the gun in toward the back direction. This is Newton’s third law in action. This is the reaction force. Due to the large mass of the gun, it moves only a small distance backward by giving a jerk at the shoulder of the gunman. The change in momentum of the gun is called recoil. Because the gun is much more enormous compared to the bullet, it does not recoil as conspicuously. The backward movement of the gun is called the recoil of the gun. You can see this whenever someone shoots a gun; they require to ground themselves to hedge alongside the recoil.
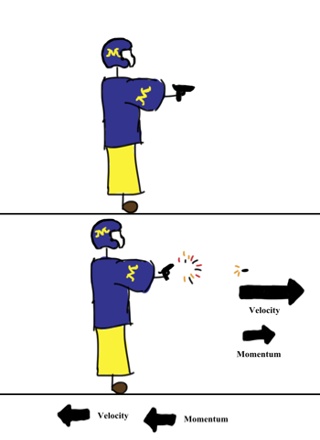
Fig: Backward Velocity of the gun and Forward Velocity of gun
This can be explained by momentum as well. Before firing both the gun and the bullet remain at rest. So the momentum of both the gun and bullet is zero. Hence their total initial momentum is zero. After firing, due to an explosion, the bullet moves ahead with a velocity. So it gets a forward momentum. Now, according to the conservation principle of momentum total momentum after firing will be zero. So, the gun will also acquire an equal and opposite momentum. Then the gun, of course, will get a backward motion [Figure].
Because of Newton’s Third Law – for each action, there is an equal and opposite reaction.
Action – the cartridge is fired. This force acts on the bullet (expelling it from the cartridge, down the barrel, and out the muzzle).
Reaction – an equivalent amount of force acts alongside the back of the chamber. You feel less force because it’s distributed over a wider region and it’s acting on a much larger object, but it’s the same amount of force.
Let the bullet of mass m is released with velocity v from a gun of mass M. Again, suppose the velocity of the gun after firing = V.
Before firing their total momentum = 0
After firing their total momentum = momentum of the gun + momentum of the bullet
= MV + mv
But according to the conservation principle momentum before and after must be equal.
so, MV + mv = 0
then, mv = – MV = M(-V)
That means, (mass of the bullet x velocity of the bullet)
= (mass of the gun x recoil velocity of the gun)
From this equation, it can be said that velocity of the bullet > recoil velocity of the gun.