Application of integration in some cases:
(i) General integration of vector quantity is similar to scalar quantity. Let the vector A→(t) = ȋ Ax(t) + ĵ Ay(t) + ƙ Az (t) be integral of a scalar variable t, then;
∫ A→(t) dt = ȋ ∫ Ax (t) dt + ĵ ∫ Ay (t) dt + ƙ ∫ Az (t) dt.
It is called the indefinite integral of A (t).
(ii) In many cases integration is opposite to differentiation: for example-
∫ cos x dx = sin x
d/dx (sin x) = cos x
i.e., if sin x is differentiated we get cos x and if cos x is integrated we get sin x.
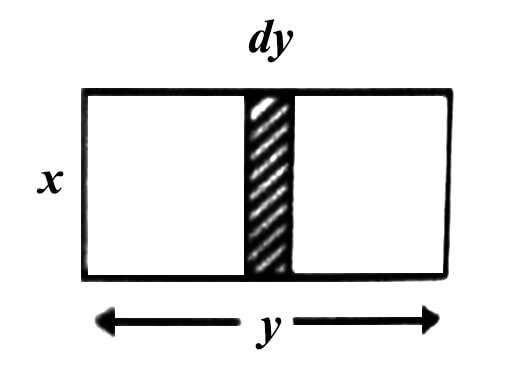
(iii) If a rectangle consists of innumerable elements of length x and width dy [Figure] then area of the rectangle will be, ∫ xdy = x∫ dy = xy
(iv) If limit of width is mentioned, then area = y∫0 x dy = x [y]y0 = x (y-0) = xy.