Application of integration in case of velocity:
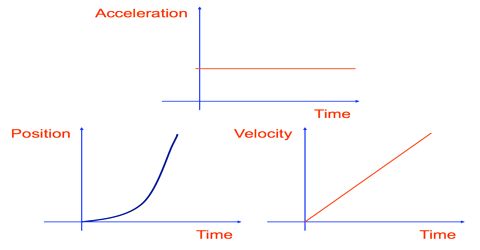
While calculating velocity of a moving body we divide displacement by total time and get velocity. This velocity is nothing but average velocity. Because, while moving at one time motion of the body is uniform and in other time it is non-uniform. So, if the moving path is divided into innumerable width or elements and each of these elements dx is divided by the time dt taken to travel this distance (element), then we can determine velocity for this element. Then if we integrate this velocity dv for the entire path we get actual velocity. It is shown below by integration;
For the element dx, velocity = dv = dx/dt.
Again for the entire path, velocity = v∫0 dv = v + c … … … (1)
If the magnitude of the velocity is definite, then by solving the above integration within that limit we get actual velocity. For example, if the magnitude of velocity is v = v from v = 0, then by integrating equation (1) total velocity is obtained.
In this case, total velocity = v∫0 dv = [v]v0 = (v – 0) = v
So, it can be said that summation of very small elements is integration. By a real example we can get the idea. For example, a person when reads news in front of the camera of the TV studio, then his picture is divided into innumerable elements, again when it reaches on the screen then those elements of the picture get united and transforms into full picture. In this case, formation of very small elements of the picture is differentiation and the process of unification of these small elements on the TV screen is integration.