Since electric currents produce magnetic fields, time-varying currents produce time-varying magnetic fields. Hence, a time-varying current in a circuit will produce a time-varying mag-netic flux through a nearby circuit loop causing an emf in that loop. The mutual inductance introduced of “Essential Electromagnetism” where it was defined as follows. Suppose you have two coils of wire at rest and you run current I1 around Coil 1 the magnetic flux due to Coil 1 through Coil 2 divided by I1 is the mutual inductance M of the two coils. For the case of time-varying currents, from Faraday’s law, the emf in Coil 2 due to a changing current in Coil 1, and the emf in Coil 1 due to a changing current in Coil 2 are
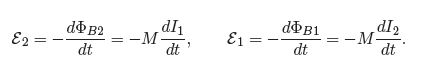
As an example of calculating the mutual inductance we consider a solenoid comprising N1 coils tightly wound around a cylindrical rod made of a material with magnetic permeability μ, and a second solenoid comprising N2 coils loosely wound around the first solenoid. It is easier to calculate the flux due to the tightly-wound solenoid through the loosely-wound solenoid, than the flux due to the loosely-wound solenoid through the tightly-wound solenoid. The magnitude of the magnetic field inside the tightly-wound solenoid is approximately
B1 (t) = μ (N1 / h) I1 (t)
and so the magnetic flux threading the N2 coils of the loosely-wound solenoid is
ϕB2 (t) = N2 Aμ (N1 / h) I1 (t)
Giving,
M = μ (N1 N2 A / h)
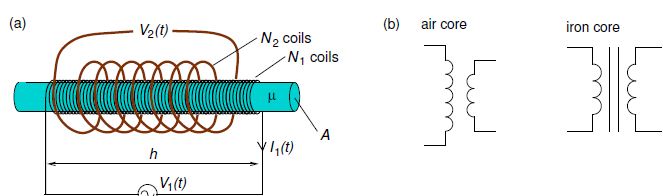
Figure: (a) Example of mutual inductance of a loosely-wound solenoid around a tightly-wound solenoid. (b) Circuit symbols for transformers.
A circuit such as that shown in Figure (a) could serve as a transformer in AC circuits as the output voltage would differ from the input voltage. Generally if the two coils share the same magnetic flux per individual coil element or “turn” the ratio of the voltage across the secondary coils (Ns turns) to that across the primary coils (Np turns) is
(Vs/VP) = (Ns/ Np)
In the example above the tightly-wound solenoid is the primary (p) and the loosely wound one is the secondary (s). To ensure the two coils share the same magnetic flux per turn, transformers may have a core made of a high permeability material, i.e. one having μ >> μ0 such as soft iron. Circuit symbols for air-core and iron-core transformers are shown in Figure (b). The core would often be in the shape of a torus to minimize magnetic flux leakage.










