Starting with Maxwell’s equations, we shall shortly derive the wave equations for the electric and magnetic fields and show that they predict the existence of electromagnetic (EM) waves in free space travelling at speed c. The relationships between the fields, the wave vector and angular frequency for a valid monochromatic EM plane wave will be determined, and the energy density, Poynting vector and wave intensity will be derived. Since monochromatic EM plane waves are an idealisation, we discuss when this may be a good approximation for quasi-monochromatic EM waves through introducing the concepts of coherence.
Here shortly show, Maxwell’s (1865) theory predicted the existence of electromagnetic waves travelling at the speed of light. Experiments by Hertz in 1886, in which he produced and detected radio waves, provided proof of Maxwell’s theory. At the time it was thought that a medium was required for propagation of EM waves. This “luminiferous aether” was supposed to be at rest while the Earth moved through it – spinning around its axis once a day while orbiting the Sun once per year, as the Sun orbits around the centre of the Galaxy, etc.
If the aether were fixed, while the Earth moved through it, then the light transit time over a fixed baseline on Earth would depend on the orientation of the baseline with respect to the “aether wind”. In 1887 Michelson and Morley, and later experimenters, found that there was actually no difference with orientation, proving that there is no aether and that EM waves can propagate without a medium. This is unique, as all other classical waves require a medium to propagate in (e.g. sound waves in air).
To show that EM waves in a vacuum are indeed allowed, we need to derive their wave equation. We will actually derive the wave equation for a charge-free and current-free linear medium. The results we obtain for this case can easily be specialised to the vacuum case by setting μ → μ0 and Ɛ → Ɛ0.
First, take the curl of Faraday’s law, giving;
Λ * (Λ * E) = Λ * (- ϐB/ϐt) = – ϐ/ϐt (Λ * B)
Next, using the 2nd derivative rule Λ x (Λ x a) = Λ(Λ • a) — V2 a we get
Λ (Λ * E) – Λ2 E = – ϐ/Ɛt (Λ * B)
Ina charge-free region Λ * E = p/Ɛ0 = 0, and we can use use Ampere’s law to replace Λ x B:
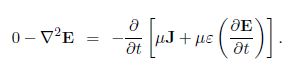
Hence, for a charge-free (p = 0) and current-free region (J = 0)
Λ2 E – μƐ (ϐ2 E/ ϐt) = 0 (wave equation for E)