One can derive the equation describing conservation of momentum from the force on a particle of charge q, as given by Lorentz force equation F = (qE ÷ qv x B). For the charges inside volume V, this becomes
dPpart/dt = ʃv (pE + J * B) d3r
where Ppart is the total momentum of the particles inside V, and we have used pv = J. Using all four of Maxwell’s equations, the integrand can be written
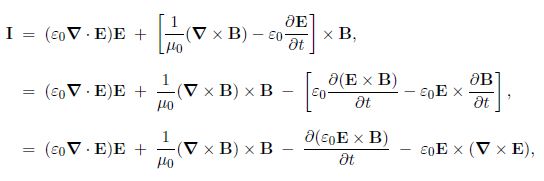
(Gauss’ law and the modified Ampere’s law were used in this equation, and Faraday’s law was used in second equation).
Re-writing this X Equation with the terms involving time-derivatives on the left hand side
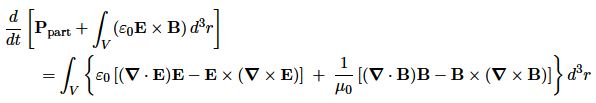
we can identify the left hand side as the rate of change of particle and field momentum in volume V, and so the electromagnetic field momentum density must be
g = Ɛ0 E * B = μ0 Ɛ0 E * H = (1/C2)S
The right had the side of Equation X must equal the rate of flow of momentum into volume V. We will see this more easily if we are able to re-write the right hand side as a flux integral with the help of Gauss’ theorem, but we must first write the integrand as the divergence of some field. But, since the rate of increase of momentum density is a vector field having 3 dimensions, the quantity we must take the divergence of will have 9 dimensions. This tensor field, Tij is called the Maxwell stress tensor, and momentum conservation in electrodynamics is expressed by
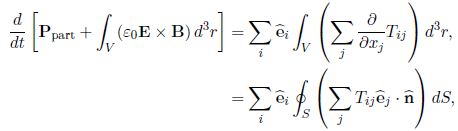
where ñ is the outward normal unit vector at surface S which bounds volume V. In Appendix B I prove that
Tij = Ɛ0 [Ei Ej + C2 Bi Bj – ½ ϐij (E*E + C2 B*B)